 確率の計算式の統計的詳細
確率の計算式の統計的詳細
この節では、「単純Bayes」の赤い三角ボタンのメニューにある[確率の計算式の保存]オプションで保存される計算式について説明します。説明変数がx1, x2, …, xpであるデータ行が、クラスCkに属する条件付き確率(事後確率)の計算式は、単純Bayes法のアルゴリズムの統計的詳細節で示されるP(Ck|(x1,..., xp))とは少し異なっています。計算式が、効率的に計算を行うために少し変形されています。
「単純 スコア」の計算式
所定のクラスCkに対する「単純 スコア」S(Ck)の計算式は、P(Ck|(x1,..., xp))における分子の式を変形したものであり、次のように計算されます。
S(Ck) = exp[ln{P(Ck)} + 連続尺度のスコア + カテゴリカルのスコア + ln(R)]
「単純 スコア」の計算式は、連続尺度の説明変数とカテゴリカルな説明変数からのスコアの組み合わせです。Rは、計算された値が小さくなりすぎることを防ぐための定数です。連続尺度の説明変数でのスコアは、次のように計算されます。
連続尺度のスコア = 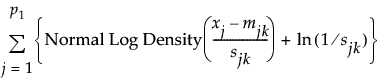
ここで
j = 1,..., p1は、連続尺度の説明変数に対する通し番号
カテゴリカルな説明変数でのスコアは、次のように計算されます。
カテゴリカルのスコア = 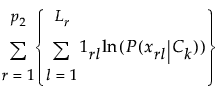
ここで
r = 1,..., p2は、カテゴリカルな説明変数に対する通し番号
l = 1,..., Lrは、r番目のカテゴリカルな説明変数に含まれる水準に対する通し番号
1rlは、xrlがr番目のカテゴリカルな説明変数のl番目の水準の場合は1、それ以外の場合は0に等しくなる指示変数です。
「単純 スコア和」の計算式
「単純 スコア和」の計算式Sは、全クラスの単純スコアを合計したものです。これは、P(Ck|(x1,..., xp))における分母に相当します。
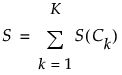
「単純 確率」の計算式
特定のクラスCkに対する「単純 確率」の計算式は、P(Ck|(x1,..., xp))です。次式により計算されます。
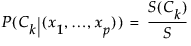
「単純 予測式」の計算式
「単純予測式」の計算式は、該当のデータ行を事後確率P(Ck|(x1,..., xp))が最大となっているクラスに分類するものです。事後確率が最大となるクラスは、「単純 スコア」が最大となっているクラスです。