等分散性検定の統計的詳細

この節では、「一元配置」プラットフォームの「等分散性の検定」レポートについて詳しく解説します。

F値

O’Brienの検定では、元の応答変数を変換して、新しい応答変数を作成し、それに対して一元配置分散分析を行います。変換後の応答変数は、そのグループ平均が、元の応答変数のグループごとの不偏分散と等しくなるように作成されます。この変換後の応答変数は、次式で計算されます。

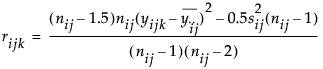
nは、観測値yijkの個数を表します。

Brown-Forsythe検定は、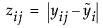に対する一元配置分散分析のF検定です。ここで、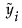はi番目の水準におけるYの中央値です。

Leven検定は、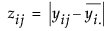に対する一元配置分散分析のF検定です。ここで、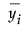はi番目の水準におけるYの平均です。

Bartlett検定は、次式により計算されます。

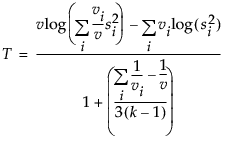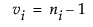この式で、および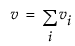

niはi番目の水準における度数、si2はi番目の水準におけるYの不偏分散です。このBartlett検定の検定統計量は、カイ2乗分布に従います。表中のBartlett検定のF値に出力されている値は、このBartlettのカイ2乗検定統計量を自由度で割ったものです。

Welchの検定のF値

Welchの検定のF値は、次の式で計算されます。

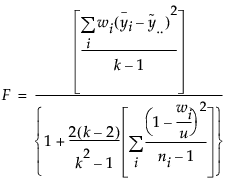この式で, ,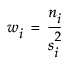

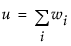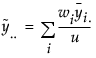
niはi番目の水準における度数、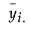はi番目の水準におけるYの平均、si2はi番目の水準におけるYの不偏分散です。

Welch検定の分母自由度

Welch検定の分母自由度は、次の近似式によって計算されます。

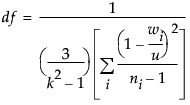
ここで、wi、ni、uはF値の式と同じ定義です。

より詳細な情報が必要な場合や、質問があるときは、JMPユーザーコミュニティで答えを見つけましょう (community.jmp.com).