公開日: 09/19/2023
一致性の統計量の統計的詳細
この節では、「分割表」プラットフォームにおける一致性の統計量について詳しく解説します。2名の評価者が、n個の対象を判定したとします。2人の判定者の判定が完全に一致している場合は、カッパ係数が1になります。観測された一致が、偶然によって一致する期待値を上回ると、カッパ係数は正の値になります。カッパ係数が大きいほど、一致性の高いことを示します。実際にはほとんどあり得ないケースですが、観測された一致性が偶然による一致性を下回ると、カッパが負になります。カッパ係数の最小値は、周辺度数に応じて-1から0までの値を取ります。
カッパ係数は、次式により計算されます。
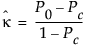 この式で、
この式で、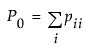 および
および 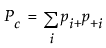
ここで、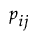 は
は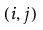 番目のセルの個体の比率であり、
番目のセルの個体の比率であり、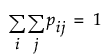 が成り立つことに注意してください。
が成り立つことに注意してください。
単純なカッパ係数の漸近分散は、次のような推定式で計算されます。
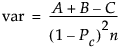 この式で
この式で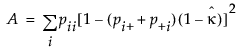 ,
, 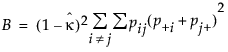 ,
,
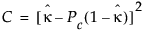
Cohen(1960)とFleiss et al.(1969)を参照してください。
対称性に対するBowker検定は、「分割表における確率が対称である(pij=pjiである)」という帰無仮説を検定します。
より詳細な情報が必要な場合や、質問があるときは、JMPユーザーコミュニティで答えを見つけましょう (community.jmp.com).