［直交のあてはめ］オプションの統計的詳細

「二変量」プラットフォームの［直交のあてはめ］オプションは、直交方向の距離の平方和を最小にするような直線をあてはめます。これは、Xの測定値にランダムなばらつきがある場合に標準的な最小2乗法より有効です。標準的な最小2乗法では、X変数が所与で、Xの関数に誤差を加えたものがY変数であると仮定されます。

メモ: 直交方向に引かれた垂線の長さは、XとYのスケールに左右されます。XとYのスケールをどのように決めるべきかということは、単なるグラフ上の問題ではなく、統計的な問題です。

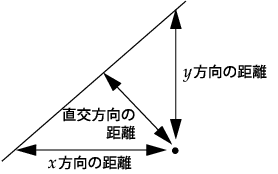
図5.22 回帰直線への垂線 

直交のあてはめを行うには、Yの誤差の、Xの誤差に対する分散比を指定する必要があります。ここで、「分散」はデータから計算される分散ではなく、誤差の母分散であることに注意してください。標準的な最小2乗法では、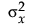が0なので、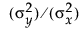の比は無限大になります。大きな分散比を指定して「直交のあてはめ」を行うと、求められた直線は、標準的な最小2乗法の回帰直線に近くなります。逆に、分散比を0にすると、YのXへの回帰ではなく、XのYへの回帰に等しい結果が得られます。

この直交のあてはめが最も使われるのは、2つの測定システム（測定器）で、同じ対象を測定したときです。この場合、XとYの測定値には、同じような種類の測定誤差があります。誤差の比は、1（等分散性）のように仮定される値であるか、測定システムに関する知識に基づいて計算されます。

信頼区間は、Tan and Iglewicz（1999）で説明されている方法で計算されます。