確率分布の統計的詳細

この節では、「工程能力分析」プラットフォームでサポートされている確率分布の確率密度関数fを紹介します。また、Johnson分布とSHASH分布を除くすべての分布の期待値と分散も紹介します。

正規

, , ,

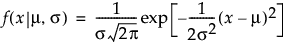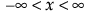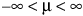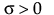
E(X) = m

Var(X) = s2

ベータ

, , ,

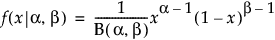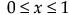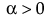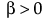
E(X) =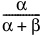

Var(X) =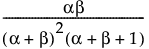

この式で、B(·)はベータ関数です。

指数

, ,

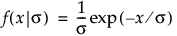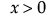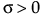
E(X) = s

Var(X) = s2

ガンマ

, , ,

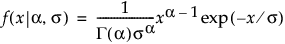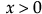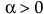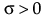
E(X) = as

Var(X) = as2

ここで、Γ(·)はガンマ関数です。

Johnson

Johnson Su

, , ,

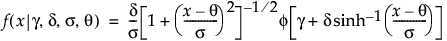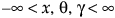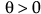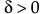
Johnson Sb

, ,

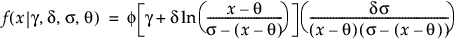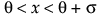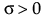
Johnson Sl

, ,

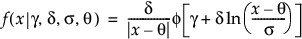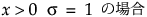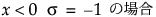
上式で、f(·)は標準正規分布の確率密度関数です。

対数正規

, , ,

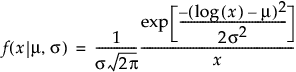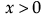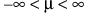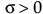
E(X) =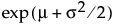

Var(X) =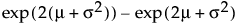

正規混合

二重正規混合分布と三重正規混合分布は、いずれも次のような確率密度関数になっています。

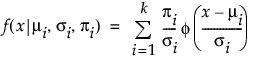
E(X) =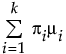

Var(X) =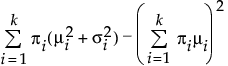

ここで、mi, si, piは、i番目のグループのそれぞれ平均・標準偏差・割合であり、f(·)は、標準正規分布の確率密度関数です。二重正規混合分布では、kは2です。三重正規混合分布では、kは3です。各正規分布の平均と標準偏差、および、全体に対する割合を推定します。

SHASH

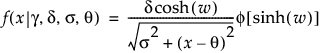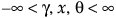, , 0 < d, 0 < s

ここで、

f(·)は標準正規分布の確率密度関数です。

メモ: g = 0、d = 1のSHASH分布は、位置、尺度がそれぞれq、sの正規分布と同じです。

Weibull

, ,

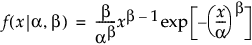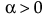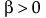
E(X) =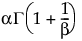

Var(X) =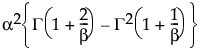

ここで、G(·)はガンマ関数です。

より詳細な情報が必要な場合や、質問があるときは、JMPユーザーコミュニティで答えを見つけましょう (community.jmp.com).