共分散行列の推定法に関する統計的詳細

ここでは、「多変量の相関」プラットフォームで、共分散行列および平均ベクトルを推定するのに使用される推定法の統計的詳細について説明します。

REML

データに欠測値がある場合、REML法（制限最尤法）は、最尤法に比べて、推定値のバイアス（偏り）が小さいのが特徴です。REML法は、誤差対比（error contrast）から導出された周辺尤度を最大化する推定方法です。REML法は、分散および共分散を推定するのによく使われます。［多変量の相関］の［REML］は、反復測定データの相関構造に無構造（unstructured）を仮定した混合モデルのREML推定と同じです。混合モデルのREML推定については、SAS Institute Inc.（2020e）の「MIXED Procedure」章を参照してください。

ロバスト

この手法では、外れ値に対して小さな重みを与えることで、外れ値が実質的に無視されます。推定において、次式により重みを反復的に計算します。

Q < Kの場合は wi = 1.0、そうでない場合は wi = K/Q

ここで、Kは、データの列数を自由度としたカイ2乗分布の75%点です。また、Qは次式により計算されます。

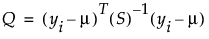
ここで、yiはi行目のデータ、mは平均ベクトルの現在の推定値、Sは共分散行列の現在の推定値です。また、Tは行列の転置を意味します。なお、各反復の最後において、分散共分散行列の推定値が不偏になるように調整が行われます。

ロバスト推定は、データに外れ値があまりない場合には、通常の推定方法に比べ、推定値のばらつきが大きくなります。しかし、データに外れ値がある場合には、通常の方法に比べて、精度が高い推定値が得られます。

より詳細な情報が必要な場合や、質問があるときは、JMPユーザーコミュニティで答えを見つけましょう (community.jmp.com).