特異値分解
特異値分解(Singular Value Decomposition; SVD)は、行列による線形変換を、回転、尺度変換、もう一つの回転で表したものです。特異値分解は、n × pの行列Xを次のように分解します。
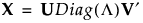
rをXのランクとします。また、r × rの単位行列をIrとします。
行列U、Diag(L)、およびVには、次のような性質があります。
Uは、U′U = Irを満たすn × rの準直交行列
Vは、V′V = Irを満たすp × rの準直交行列
Diag(L)は、列ベクトルL = (l1, l2, ..., lr)′を対角要素に持つr × rの対角行列。ここで、l1 ≥ λ2 ≥ ... ≥ λr > 0
liは、Xの0以外の特異値です。
特異値分解は、正方行列のスペクトル分解(固有値分解)と次のような関係があります。
• liの2乗は、X′Xの0以外の固有値です。
• Vのr列は、X′Xの固有ベクトルです。
メモ: 行列U、V、および特異値に関し、行列の次元に応じていくつかの異なる表現方法が文献で紹介されています。しかし、それらには、Xのランクまでの特異値分解に関しては根本的な違いはありません。
特異値分解の詳細については、Press et al.(1998, Section 2.6)を参照してください。
共分散行列
ここでは、特異値分解によって共分散行列の固有ベクトルと固有値を求める方法について説明します。対象の共分散行列が巨大であるがランクが小さい場合には、データを特異値分解したほうが、共分散行列を固有値分解するよりもずっと効率的です。
nをオブザベーション数、pを変数の個数とします。データのn × p行列をXとします。
特異値分解は通常、標準化されたデータに適用されます。データの標準化とは、データから平均を引き、それを標準偏差で割る変換を指します。標準化したデータのn × pをXsで表します。そうすると、標準化されたデータの共分散行列はXの相関行列になります。その共分散行列(相関行列)は、次式のように表されます。
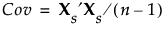
Xsの特異値分解によって、Xs′Xsの固有ベクトルと固有値を求めることができます。この性質を利用すれば、行列Xが非常に横長の場合(列数が膨大な場合)、または縦長の場合(行数が膨大な場合)に、固有ベクトルや固有値を効率的に計算できます。この計算方法が、横長データに対する主成分分析の基本になります。「「主成分分析」レポート」を参照してください。
共分散行列の逆行列
一部の多変量分析では、共分散行列の逆行列を計算する必要があります。ここでは、特異値分解によって共分散行列の逆行列を計算する方法について説明します。
標準化したデータ行列をXsとし、また、S = Xs′Xsとします。特異値分解された行列は、Sと次のような関係になっています。
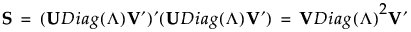
Sがフルランクの場合、Vはp x pの直交行列で、S-1は次のように表されます。
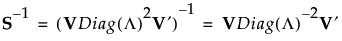
Sがフルランクではない場合、Diag(L)-1は一般化逆行列、Diag(L)+に置き換えられます。これらの逆行列や一般化逆行列は、Diag(L) の対角要素をその逆数に置き換えたものです。これにより、Sの一般化逆行列は次のように定義されます。
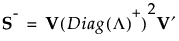
この一般化逆行列は、特異値分解だけによって求めることができます。
横長データの線形判別分析における特異値分解の適用については、横長データに対する線形判別法を参照してください。
特異値分解の計算
JMPの「多変量分析」プラットフォームで使われている特異値分解のアルゴリズムは、Golub and Kahan(1965)が提唱したものに従っています。Golub and Kahan(1965)の手法は、2つのステップから成ります。最初のステップでは、行列Mを2重対角行列Jに変形します。2番目のステップで、Jの特異値を計算します。この特異値は、元の行列Mの特異値と同じです。行列Mの列は、通常、計算における列の効果を均一化するために標準化されます。Golub and Kahan(1965)の手法は、計算が効率的です。