超越関数
Arrhenius(n)
説明
温度nを、Arrheniusモデルにおける説明変数の値に変換する。
戻り値
11604.5181215503/(n+273.15)
引数
n
温度（単位は摂氏）。
メモ
これは頻繁に使用される変換の1つです。
Arrhenius Inv(n)
説明
Arrenhius関数の逆関数。値nを摂氏の温度に変換する。
戻り値
(11604.5181215503/n)-273.15
引数
n
Arrheniusモデルにおいて説明変数の値に変換された値。
メモ
これは頻繁に使用される変換の1つです。
Beta(a, b)
説明
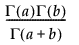
戻り値
ベータ関数
引数
a, b
数値
Cytometry Logicle(x, T, W, M, A)
説明
サイトメトリーLogicle変換を計算する。Logicle変換の詳細については、Moore and Parks（2012）を参照してください。
Cytometry Logicle Inverse(y, T, W, M, A)
説明
逆サイトメトリーLogicle変換を計算する。Logicle変換の詳細については、Moore and Parks（2012）を参照してください。
Digamma(n)
説明
ガンマ関数（LGamma）の対数の導関数。
戻り値
nにおけるディガンマ関数の値
引数
n
数値。
Exp(a)
説明
eをa乗する。
戻り値
ea
引数
a
数値。
等価表現
e()^a
ExpM1(x)
説明
Exp(x)-1を戻す。xが非常に小さい場合に、より正確な計算結果を戻します。
Factorial(n)
説明
1からnまでの全整数を掛ける。
戻り値
nの階乗
引数
n
任意の整数。
メモ
指定できる引数は1つだけです。
FFT({list }, <named arguments>)
説明
行列のリストに対して高速Fourier変換（FFT）を行う。
戻り値
複素数を表す1つまたは複数の行列のリストを引数とし、その最初の引数と同じ次元の、2つの行列のリストを戻す。
引数
List
1つまたは2つの行列を含むリスト。1つの行列で構成されている場合、その行列は実数とみなされます。2つの行列で構成されている場合、1番目は実数、2番目は虚数部分とみなされます。2つの行列は次元が同じで、どちらも行が2つ以上なければなりません。
オプションの名前付き引数
<<inverse(Boolean)
1（真）の場合、逆FFTが実行される。
<<multivariate(Boolean)
1（真）の場合、単変量FFTが1列ごとに実行される。0（偽）の場合、空間FFTが実行される。
<<scale(number)
戻り値にnumberで指定した乗数を掛け合わせる。
Fit Transform To Normal(Distribution("name"), Y(vector), <Freq(vector))
説明
データのベクトルに対し、正規分布へと変換するための分布をあてはめる。Johnson Sl、Johnson Sb、Johnson Su、一般化対数（GLog）といった分布をあてはめることができます。
戻り値
パラメータ推定値、共分散行列、対数尤度、AICc、収束メッセージ、変換値で構成されるリスト。『基本的な回帰モデル』の尤度・AICc・BICを参照してください。
Gamma(t, <limit>)
説明
xに対するガンマ関数の値を戻す。
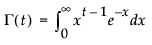
戻り値
ガンマ関数の値
引数
t
数値または列。
limit
（オプション）上限。デフォルトは∞。
メモ
Gamma(t, limit)はGamma(t)と積分される式は同じですが、積分の範囲における上限を無限ではなくlimitとします。
LGamma(t)
説明
tの対数ガンマ関数（ガンマ関数の自然対数）を戻す。
Ln(n)
説明
nの自然対数（底eの対数）を戻す。
Log(n, <base>)
説明
nの自然対数（底eの対数）を戻す。オプションの第2引数を追加すると、別の底を指定できます。たとえば、Log(n,3)は、3を底とするnの対数です。Logの引数は、任意の数式をとることができます。式Log(e())は1、Log(32,2)は5です。
Log10(n)
説明
nの常用対数（底は10）を戻す。
Log1P(n)
説明
xがきわめて小さいときに精度がより高くなることを除けば、Log(1 + x)と同じ。
Logist(x)
説明
1/(1+Exp(-x))を戻す。定義域（-∞～+∞）が0～1に変換されます。この関数は、ロジスティック回帰に役立ちます。
Logist Percent(p)
説明
Logist()関数の結果を0～100のスケールで戻す。
Logit(p)
説明
log(p/(1-p))を戻す。
Logit Percent(p)
説明
Logit()関数と似ているが、引数を0～1ではなく0～100で指定する。
N Choose K(n, k)
説明
この関数は、一度にn個のうちからk個を選択する場合の組み合わせの数（「nCk」）を戻す。この組み合わせの数は、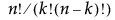
のように階乗を使った式で計算することができます。たとえば、NChooseK(5,2)は10になります。
メモ
この関数の計算において、JMPではLGamma関数が内部的に使用されています。そのため、結果は必ずしも整数とは限りません。
Power(a, <b>)
a^b
説明
aをb乗する。
戻り値
aをb回掛け合わせた積
引数
a
変数、数値、または行列。
b
（オプション）変数または数値。
メモ
Power()の場合、第2引数（b）はオプションで、デフォルト値は2です。Power(a)はa2を戻します。
Root(n, <r>)
説明
nのr次の根を戻す。デフォルトではrが2で、平方根を戻します。
SbInv(z, gamma, delta, theta, sigma)
説明
標準正規分布の変数を上下に有界なJohnson Sb分布の変数に変換する。
SbTrans(x, gamma, delta, theta, sigma)
説明
上下に有界なJohnson Sb分布の変数を標準正規分布の変数に変換する。
Scheffe Cubic(x1, x2)
説明
x1*x2*(x1-x2)の結果を戻す。3次の配合モデルの表記に対応しています。
SHASHInv(z, gamma, delta, theta, sigma)
説明
標準正規分布の変数をsinh-arcsinh（SHASH）分布の変数に変換する。変換は、s*sinh((arcsinh(z)-g)/d)+qの式で計算されます。
SHASHTrans(x, gamma, delta, theta, sigma)
説明
sinh-arcsinh（SHASH）分布の変数を標準正規分布の変数に変換する。変換は、sinh(g+d*arcsinh((x-q)/s))の式で計算されます。
SlInv(z, gamma, delta, theta, sigma)
説明
標準正規分布の変数をJohnson Sl分布の変数に変換する。
SlTrans(x, gamma, delta, theta, sigma)
説明
Johnson Sl分布の変数を標準正規分布の変数に変換する。
Sqrt(n)
説明
nの平方根を戻す。
Squash(expr)
説明
関数1/ [1 + exp(expr)]を効率よく計算する。
Squish(expr)
説明
Squash(-expr)または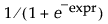
と同じ。
SuInv(z, gamma, delta, theta, sigma)
説明
標準正規分布の変数を有界でないJohnson Su分布の変数に変換する。
SuTrans(x, gamma, delta, theta, sigma)
説明
有界でないJohnson Su分布の変数を標準正規分布の変数に変換する。
Trigamma()
説明
nにおけるトリガンマ関数の値を戻す。トリガンマ関数はディガンマ関数の導関数です。