潜在变量增长曲线模型的示例
潜在变量增长曲线 (LGC) 模型支持分析人员对纵向数据进行建模,并描述随时间变化的轨迹特征。最常见的潜在变量增长曲线模型是线性增长模型,其中指定了截距和斜率潜在变量,以捕获过程的总体轨迹以及单个观测与总体轨迹的偏差。该模型非常类似于随机系数模型。LGC 模型的一个关键特性是它们对数据的均值结构施加约束。对均值结构建模支持您检验与增长相关的假设。
在本例中,您使用多项选择测试得分对参与一项学习计划 4 年以上的学生的成绩得分进行建模。您想要检验以下假设,即:线性轨迹可描述该过程的特征。
1. 选择帮助 > 样本数据文件夹,然后打开 Academic Achievement.jmp。
2. 选择分析 > 多元方法 > 结构化方程模型。
3. 从多项选择年份1 一直选择到多项选择年份4,然后点击模型变量。
4. 点击确定。
“结构化方程模型”报表“模型规格”分级显示项随即显示。
5. 选择模型快捷方式 > 纵向分析 > 线性潜在变量增长曲线。
“模型规格”关系图现在显示线性潜在变量增长曲线模型。
6. 点击“视图”面板框中列表选项卡。
7. 选择“方差”列表中的前 4 项,然后点击设置等于。
这会将每个变量的残差方差限制为相等,这类似于方差齐性假设。在 SEM 中,该假设是可检验的,这样另一个模型可以在没有等式约束的情况下进行拟合,并与卡方差异检验进行比较。
8. 在“模型名称”下方的文本框中,键入“方差相等的线性 LGC”。
9. 点击运行。
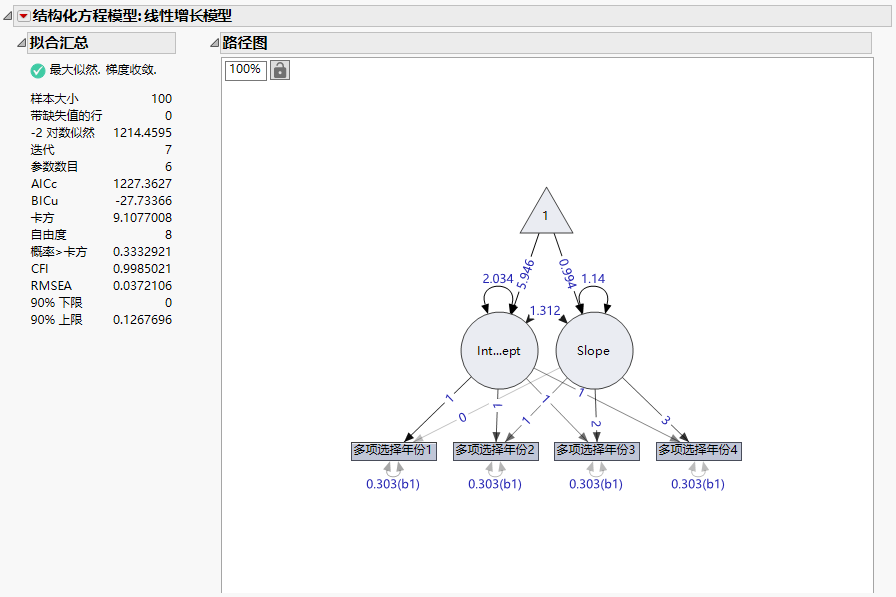
图 8.11 线性 LGC 模型的拟合汇总和路径图
“拟合汇总”报表中列出的该模型的卡方统计量为 9.11,自由度为 8。请注意,相应的 p 值为 0.3333,该值不显著。这表明,没有证据可以拒绝模型拟合良好这一原假设。因此,您可以得出结论:该模型对数据拟合良好。CFI 和 RMSEA 拟合指数也指示拟合极佳,因为它们分别大于 0.9 和小于 0.1。
图 8.12 线性 LGC 模型的参数估计值
截距的均值估计值为 5.95,这指示第一年的总体成绩得分。这意味着,在第一次测量时,学生的学习成绩平均为 5.96。截距的均值以第一次为中心,因为斜率因子在该变量上的载荷为零。
斜率的均值估计值为 0.99,这表明总体成绩得分每年增加 0.99。截距和斜率因子的显著方差估计值指向平均轨迹周围的显著变异性;并不是每个人的起点都一样,每个人的增长速度也都不尽相同。外部变量可以用作截距和斜率的预测变量,以了解导致个体轨迹差异的原因。
最后,截距和斜率之间的正协方差表明,那些第一年学习成绩较高的学生往往会随着时间的推移成绩进步更快。
LGC 模型为调查过程如何随时间变化提供了一种灵活的方法。“模型快捷方式”菜单提供了可相互拟合和检验的备选轨迹,以确定最佳模型拟合,包括无增长轨迹、二次轨迹,甚至是非线性轨迹(使用“潜在基函数”选项)。