用于量度的公式

覆盖率和多样性是为覆盖阵列设计计算的两个量度。计算覆盖率和多样性的公式取决于是否存在组合约束。将使用以下符号：

uCv 是从 u 个元素中一次选取 v 个元素的所有组合数

t 是设计的强度

K 是因子数

M = KCt

i = 1, 2, ..., M 是对 t 个因子的所有组合（或投影）进行排序的索引

vik 是第 k 个因子的水平数

ni 是设计中针对第 i 个投影的非重复 t 元组数

pi 是第 i 个投影中的因子的 vik 乘积

r 是设计中的试验次数

无约束设计

覆盖率和多样性分别用以下公式计算：

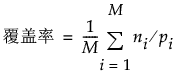
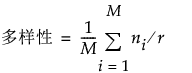
受约束设计

在受约束设计中，不允许某些特定的 t 元组。这可能导致某些 t 元组缺失值。对于 t 个因子的某些组合，可能根本不存在有效的 t 元组。覆盖率和多样性必须按照可能的有效组合来定义。因此，受约束设计的公式需要使用其他符号：

ai 是因第 i 个投影中的因子产生的无效 t 元组数

m 是不存在有效 t 元组的投影数

qi 是设计中包含第 i 个投影中的任何因子的缺失值的试验次数

ri = r - qi

M ′ = M - m

覆盖率和多样性分别用以下公式计算：

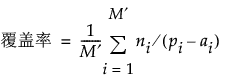
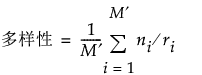
若不存在无效 t 元组 (M′ = M) 且不存在缺失值（对所有 i 均有 ri = r），则受约束设计的覆盖率和多样性定义可简化为无约束设计的定义。请参见 Morgan (2014)。

需要更多信息？有问题？从 JMP 用户社区得到解答 (community.jmp.com).