双独立样本均值的功效
使用“双独立样本均值的功效分析器”可确定关于两个组的均值的假设检验的样本大小。选择实验设计 > 样本大小分析器 > 功效 > 双独立样本均值的功效。探索在样本大小、功效、显著性和假设的待检差值之间如何权衡。样本大小与功效与以下假设检验相关联:
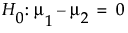
与双侧备择假设:
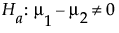
或与单侧备择假设:
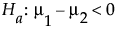 或者
或者 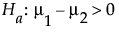
其中 m1 和 m2 是两个总体的真实均值。假定相关总体服从正态分布,且您要检测两个均值之间的差值 d。
“双独立样本均值的功效分析器”设置
使用单选按钮、文本框和菜单设置研究假设并探索样本大小。对设置进行更改时,刻画器随之更新。或者,通过拖动刻画器曲线上的十字准线来更改设置。
检验类型
指定单侧或双侧假设检验。
初步信息
Alpha
I 类误差的概率,即当原假设为真时拒绝原假设的概率。它通常是指检验的显著性水平。默认 alpha 水平为 0.05。
组总体标准差
指定计算的分布。
是
指定已知组标准差,计算使用 z 分布。
否
指定未知组标准差,计算使用 t 分布。
“双独立样本均值的功效分析器”刻画器
该刻画器支持您直观演示假设的样本大小对于功效计算的影响。
总样本大小
指定您实验中需要的总观测数(试验、实验单元或样本)。选择锁定以锁定总样本大小。
对下列对象求解:
支持您求解样本大小、待检差值或假定组标准差。
功效
指定当原假设为假时拒绝原假设的概率。在其他所有参数保持不变时,功效随着样本大小的增加而增加。
组 1 样本大小
指定您实验中的“组 1”需要的总观测数(试验、实验单元或样本)。
组 2 样本大小
指定您实验中的“组 2”需要的总观测数(试验、实验单元或样本)。
待检差值
指定组均值之间的最小差值,您希望能称为在统计上显著。
组 1 标准差 (s1)
为其中一个组“组 1”指定假定的标准差。误差标准差的估计值可以是先前的模型拟合的均方根误差 (RMSE)。
组 2 标准差 (s2)
为第二个组“组 2”指定假定的标准差。误差标准差的估计值可以是先前的模型拟合的均方根误差 (RMSE)。
注意:调整一个组的样本大小也会调整总样本大小,除非总样本大小被锁定。在这种情况下,调整一个组的样本大小也会调整另一个组的样本大小。使用文本框指定组样本大小。
“两个独立样本均值的功效分析器”选项
“分析器”红色小三角菜单和报表按钮提供更多选项:
模拟数据
打开基于分析器设置的模拟数据的数据表。查看所用设置的模拟响应列公式。
制作数据收集表
创建可用于数据收集的新数据表。该表包含有助于数据分析的脚本。
保存设置
将当前设置保存至“已保存设置”表。这样您就可以保存一套备选研究计划。请参见样本大小分析器中的已保存设置。
帮助
打开 JMP 帮助。
双独立样本均值的功效分析器的统计详细信息
检验两个样本组均值差值的功效计算基于传统的 t 检验;若 s1 和 s2 已知,则基于 z 检验。
方差未知
对于组方差未知的情况,假定 s1=s2=s,则功效计算基于备择假设的形式。对于单侧、更高备择假设 (m1 > m2):
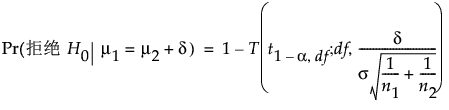
对于单侧、更低备择假设 (m1 < m2):
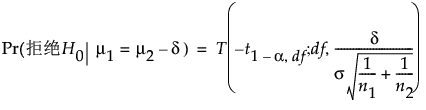
对于双侧备择假设 (m1 ≠ m2):
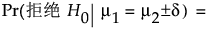
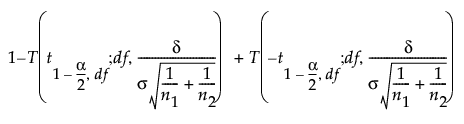
其中:
a 是显著性水平。
n1 和 n2 是组样本大小
s 是合并标准差
d 是待检差值。
t1-α,n 是自由度为 n 的中心 t 分布的第 (1 - a) 分位数
T(t; n, l) 是自由度为 n 且非中心参数为 l 的非中心 t 分布的累积分布函数。
自由度是近似自由度,也称为 Satterthwaite 自由度:
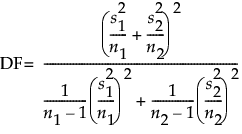
方差已知
当 s1 和 s2 已知时,z 分布用于功效计算。基于备择假设的形式计算功效。对于单侧、更高备择假设 (m1 > m2):
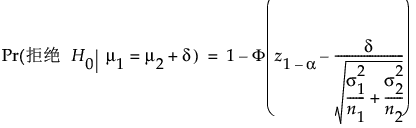
对于单侧、更低备择假设 (m1 < m2):
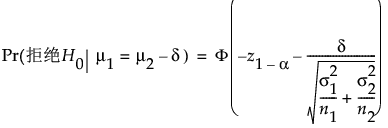
对于双侧备择假设 (m1 ≠ m2):
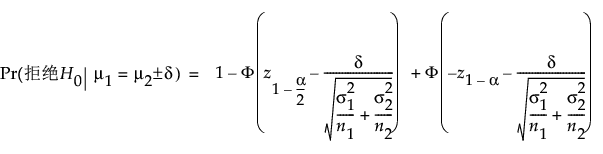
其中:
a 是显著性水平。
n1 和 n2 是组样本大小
s1 和 s2 是已知的组标准差
d 是待检差值。
z1-α 是 z 分布的第 (1 - a) 分位数
F(x) 是正态分布的累积分布函数。