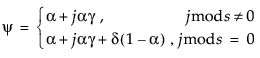指数平滑模型的统计详细信息
按以下方式定义平滑模型:
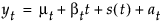
其中
mt 是时变均值项
bt 是时变斜率项
s(t) 是 s 时变季节性项中的一项
at 是随机扰动项
没有趋势的模型具有 bt = 0,非季节性模型具有 s(t) = 0。按以下方式定义这些时变项的估计量:
Lt 是估计 mt 的平滑水平
Tt 是估计 bt 的平滑趋势
St - j(j = 0, 1,..., s - 1)是 s(t) 的估计值
每个平滑模型定义一组递归平滑方程,用于描述这些估计量的变化过程。平滑方程是由被称为平滑权重的模型参数定义的:
a 是水平平滑权重
g 是趋势平滑权重
j 是趋势阻尼权重
d 是季节性平滑权重
当这些参数以不同方式进入每个模型(或根本不进入模型)时,它们具有共同的性质,即较大的权重对于最近数据有更大的影响,而较小的权重对最近数据有更小的影响。有关平滑权重的详细信息,请参见《SAS/ETS 15.2 用户指南》(“预测过程详细信息”一章)。
简单指数平滑
简单指数平滑的模型为 yt = mt + at。
根据单个平滑权重 a 来定义平滑方程 Lt = ayt + (1 – a)Lt-1。该模型等价于满足以下条件的 ARIMA(0, 1, 1) 模型:
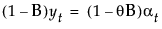 其中,
其中,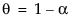
模型的移动平均形式定义如下:
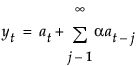
二次 (Brown) 指数平滑
双指数平滑模型为 yt = mt + b1t + at。
具有单个平滑权重 a 的平滑方程定义如下:
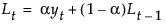
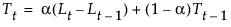
该模型等价于满足以下条件的 ARIMA(0, 1, 1)(0, 1, 1)1 模型:
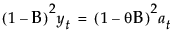 ,其中
,其中 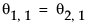 且
且 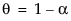
模型的移动平均形式定义如下:
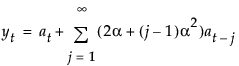
线性 (Holt) 指数平滑
线性指数平滑模型为 yt = mt + btt + at。
具有平滑权重 a 和 g 的平滑方程定义如下:
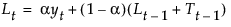
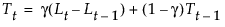
该模型等价于满足以下条件的 ARIMA(0, 2, 2) 模型:
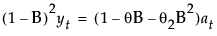 ,其中
,其中 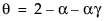 且
且 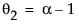
模型的移动平均形式定义如下:
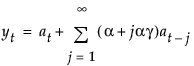
阻尼趋势线性指数平滑
阻尼趋势线性指数平滑模型为 yt = mt + btt + at。
具有平滑权重 a、g 和 j 的平滑方程定义如下:
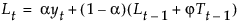
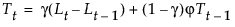
该模型等价于满足以下条件的 ARIMA(1, 1, 2) 模型:
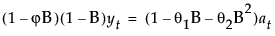
其中
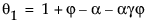
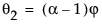
模型的移动平均形式定义如下:
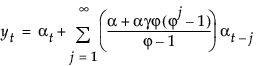
季节性指数平滑
季节性指数平滑模型为 yt = mt + s(t) + at。
具有平滑权重 a 和 d 的平滑方程定义如下:
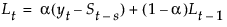
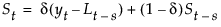
该模型等价于一个季节性 ARIMA(0, 1, s+1)(0, 1, 0)s 模型:
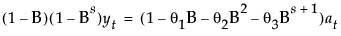
其中
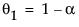
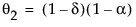
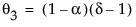
模型的移动平均形式定义如下:
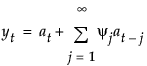 其中,
其中,
Winters 方法(加法)
Winters 方法的加法版本的模型为 yt = mt + btt + s(t) + at。
具有权重 a、g 和 d 的平滑方程定义如下:
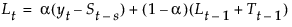
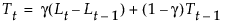
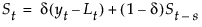
该模型等价于按以下方式定义的一个季节性 ARIMA(0, 1, s+1)(0, 1, 0)s 模型:
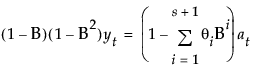
模型的移动平均形式定义如下:
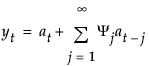
其中