“拟合正交”选项的统计详细信息

在“二元”平台中，您可以使用“拟合正交”选项拟合将垂直差值的平方和最小化的线条。当 X 的测量值存在随机变化时，这种方法要优于标准最小二乘法。标准最小二乘法拟合假定 X 变量不变，Y 变量是 X 的函数加上误差。

注意：垂直距离取决于 X 和 Y 如何按比例调整，并且如何将垂线按比例调整是一个统计问题而不是图形问题。

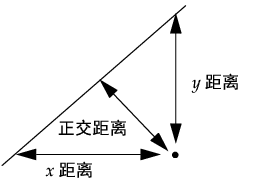
图 5.22 垂直于拟合线的线 

该拟合要求指定 Y 中的误差与 X 中的误差的方差比。这是误差的方差，不是抽样点的方差，所以您必须仔细选择。在标准最小二乘法中，比率 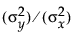是无限的，因为 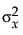为零。具有较大误差比的正交拟合将接近于标准最小二乘拟合线。若指定比率为零，拟合等价于 X 对于 Y 的回归，而不是 Y 对于 X 的回归。

该方法最常用于比较在测量同一值时均存在误差的两个测量系统。因此，Y 响应误差和 X 测量值误差均为同一类型的测量值误差。误差比是一个假设值，例如 1（方差相等），或者可以基于对测量系统的了解。

置信限按照 Tan and Iglewicz (1999) 中所述计算。