梯度下降算法的统计详细信息

使用基于 Barnes-Hut 近似 (van der Maaten, 2014) 的梯度下降算法最小化 t-SNE 方法中使用的 Kullback-Leibler 散度。该算法使用以下符号：

X = {x1, x2,..., xn} 包含 n 个数据点的原始高维数据

p = 困惑度参数

T = 迭代次数

η = 学习率

tinflate = 迭代次数，在该次数之后动量值发生更改

a(t) = 迭代 t 处的动量，其中 a(t) = 0.5（对于 t ≤ tinflate），其他情况下 a(t) = 0.8

Y(t) = {y1, y2,..., yn} 迭代 t 处的低维映射解

梯度下降算法的步骤定义如下：

1. 计算 pj|i，高维空间中的配对相似性。基于指定的困惑度 p 选择 σi。

2. 计算 pij。

3. 设置初始解 Y(0) = {y1, y2,..., yn}，初始解从均值为 0 且标准差为 10-4 的正态分布生成。

4. 对于 t = 1 到 T：

‒ 计算 qij，低维映射中的配对相似性。

‒ 计算成本函数：

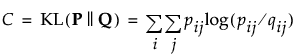
‒ 使用 Barnes-Hut 近似计算梯度函数：

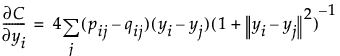
‒ 更新解：

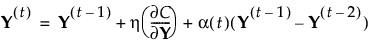
若满足以下条件之一，算法即停止：

• i 上的最大梯度值小于启动窗口中指定的收敛准则。

• 达到了最大迭代次数 T。

需要更多信息？有问题？从 JMP 用户社区得到解答 (community.jmp.com).