Stress 函数的统计详细信息

在“多维尺度化”平台中，使用 Quasi-Newton 优化法通过最小化 Stress 函数来确定 MDS 坐标。这种最小化会根据拟合前确定的维数生成一组坐标值，以最小化多维空间里对象间的派生的邻近性测度值。若数据为有序型，则使用单调回归。否则使用标准最小二乘回归。

使用以下符号定义 Stress：

• i, j - 对象数的下标

• dij - 对象 i 与 j 之间的派生距离

dij - 对象 i 与 j 之间的观测相对距离

• f(drs) - 距离的变换函数

Stress 函数定义如下：

Stress =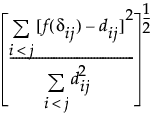

这一 Stress 测度亦称 Kruskal Stress I 型，或简称 Stress1。

需要更多信息？有问题？从 JMP 用户社区得到解答 (community.jmp.com).