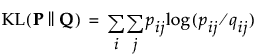t-SNE 方法的统计详细信息
通过将 {xi, xj} 的高维相似性与 {yi, yj} 的低维相似性之间的差异最小化,t-SNE 方法将高维空间 {x1, x2,..., xn} 中的点映射到低维空间 {y1, y2,..., yn} 中的点。配对相似性表示为概率分布。在高维空间中,使用高斯分布计算条件概率 pj|i。“多元嵌入”平台提供两种计算条件概率的方法。
条件概率的稀疏近似计算
若在启动窗口中选定“稀疏”选项,则使用稀疏近似来计算 pj|i。对于 n 个输入中的每一项,都使用有利点 (VP) 树发现一组最近邻。然后,仅为最近邻的那些子集计算条件概率:
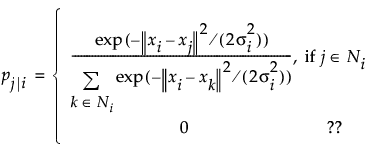
在该等式中,Ni 是 xi 的 floor(3p) 最近邻集合,其中 p 是在启动窗口中定义的困惑度参数。高斯分布的方差 σi 也基于该困惑度参数。请参见 van der Maaten and Hinton (2008) 和 van der Maaten (2014)。
条件概率的非稀疏计算
若在启动窗口中未选定“稀疏”选项,则为所有点计算 pj|i:
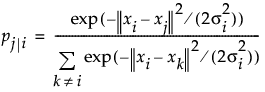
在该计算中,高斯分布的方差 σi 也基于该困惑度参数。
联合概率分布的计算
在 t-SNE 方法中,假定条件概率是对称的。因此,高维空间中的联合概率 pij 由对称条件相似性定义:
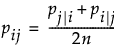
其中,对于所有 i 和 j,pij = pji。由于关注的是配对相似性,因此还假设 pii = 0。
使用自由度为 1 的 Student t 分布计算低维映射中的联合概率 qij:
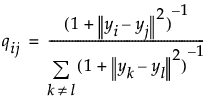
这些概率具有与 pij 相同的属性,这意味着对于所有 i 和 j,qij = qji,并且 qii = 0。
通过最小化联合概率分布 P 与联合概率分布 Q 之间的单个 Kullback-Leibler 散度,t-SNE 方法将高维空间中配对相似性与低维空间中配对相似性之间的差异最小化。P 与 Q 之间的 Kullback-Leibler 散度计算如下;