拟合测度汇总
本节介绍“结构化方程模型”平台中报告的拟合测度的汇总。
AICc、BIC 和 BICu
AICc 和 BIC 定义如下：
AICc =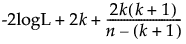
BIC =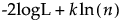 
其中：
-2logL 是负对数似然的两倍。
n 是样本大小。
k 是参数个数。
有关“模型比较”报表中基于似然的测度的详细信息，请参见《拟合线性模型》中的“似然、AICc 和 BIC”。
与不受限模型 (BICu) 相关的 BIC 定义如下：
BICu =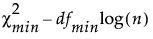 
其中：
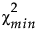是拟合模型的卡方统计量。
dfmin 是拟合模型的自由度。
n 是样本大小。
拟合模型的 BICu 等价于拟合模型的 BIC 减去不受限模型的 BIC。有关与不受限模型相关的 BIC 的详细信息，请参见 Bollen et al.(2014)。
CFI
比较拟合指数 (CFI) 定义如下：
CFI =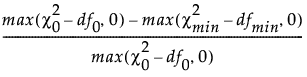 
其中：
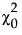是独立模型的卡方统计量。
df0 是独立模型的自由度。
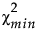是拟合模型的卡方统计量。
dfmin 是拟合模型的自由度。
有关 CFI 的详细信息，请参见 Bentler (1990)。
RNI
相对非中心指数 (RNI) 定义如下：
RNI =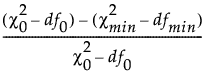 
其中：
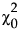是独立模型的卡方统计量。
df0 是独立模型的自由度。
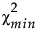是拟合模型的卡方统计量。
dfmin 是拟合模型的自由度。
有关 RNI 的详细信息，请参见 McDonald and Marsh (1990)。
TLI
Tucker-Lewis 指数 (TLI) 定义如下：
TLI =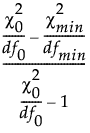 
其中：
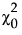是独立模型的卡方统计量。
df0 是独立模型的自由度。
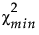是拟合模型的卡方统计量。
dfmin 是拟合模型的自由度。
详细信息，请参见 West et al.(2012)。
NFI
Bentler-Bonett 规范拟合指数 (NFI) 定义如下：
NFI =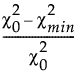 
其中：
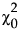是独立模型的卡方统计量。
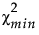是拟合模型的卡方统计量。
详细信息，请参见 West et al.(2012)。
修正的 GFI 和修正的 AGFI
修正的拟合优度指数（修正的 GFI）定义如下：
修正的 GFI =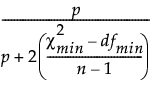 
其中：
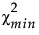是拟合模型的卡方统计量。
dfmin 是拟合模型的自由度。
p 是拟合模型的观测变量数。
n 是样本大小。
修正的拟合优度指数（修正的 AGFI）定义如下：
修正的 AGFI =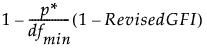 
其中：
p* 是协方差矩阵中唯一条目数和观测变量的均值向量。
dfmin 是拟合模型的自由度。
有关详细信息，请参见 Maiti and Mukherjee (1991) 和 West et al.(2012)。
RMSEA
近似的均方根误差 (RMSEA) 定义如下：
RMSEA =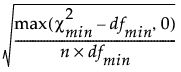 
其中：
n 是样本大小。
dfmin 是拟合模型的自由度。
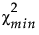是拟合模型的卡方统计量。
利用非中心卡方分布的累积分布函数 F(x|l, d) 计算 RMSEA 的置信限。90% 置信限计算如下：
下限 =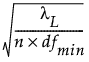 
上限 =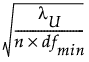 
其中：
lL 满足 F(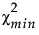
|lL, dfmin) = 0.95。
lU 满足 F(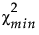
|lU, dfmin) = 0.05。
详细信息，请参见 Maydeu-Olivares et al.(2017) 中的表 J.1a、J.1b、J.6a 和 J.6b。
RMR 和 SRMR
RMR 和 SRMR 的公式定义如下：
RMR =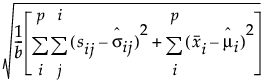 
SRMR =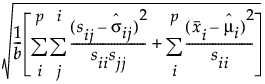 
其中：
p 是显变量数。
b 是观测变量的协方差矩阵和均值向量中的唯一条目数：
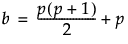
sij 是输入协方差矩阵的第 (i, j) 个元素。
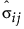是预测协方差矩阵的第 (i, j) 个元素。
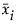是样本均值向量的第 i 个元素。
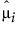是向量预测均值的第 i 个元素。
有关详细信息，请参见 SAS Institute Inc.(2020b) 中的“CANDISC 过程”一章。