奇异值分解
奇异值分解 (SVD) 允许您先后通过一次旋转、一次缩放以及另一次旋转的方式来表示任意线性变换。SVD 规定任何 n x p 的矩阵 X 可表示为:
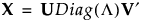
用 r 表示 X 的秩。用 Ir 表示 r x r 单位矩阵。
矩阵 U, Diag(L) 和 V 具有以下属性:
U 是 n x r 半正交矩阵且 U′U = Ir
V 是 p x r 半正交矩阵且 V′V = Ir
Diag(L) 是 r x r 对角矩阵,其正对角线元素由列向量 L = (l1, l2, ..., lr)′ 给出,其中 l1 ≥ λ2 ≥ ... ≥ λr > 0。
li 是 X 的非零奇异值。
下面说明了 SVD 与正方形矩阵的谱分解的关系:
• li 的平方是 X′X 的非零特征值。
• V 的 r 列是 X′X 的特征向量。
注意:在文献中有关于矩阵 U、V 以及包含奇异值的矩阵的维度的各种约定。但是,这些约定差异在 X 秩的范围内对分解没有实际影响。
有关奇异值分解的详细信息,请参见 Press et al.(1998, Section 2.6)。
协方差矩阵
本节说明如何使用奇异值分解 (SVD) 获取协方差矩阵的特征向量和特征值。关注的矩阵具有至少一个大的维度时,计算 SVD 比计算它的协方差矩阵和特征值分解高效得多。
用 n 表示观测数,用 p 表示关注的多元分析中涉及的变量数。用 X 表示数据值的 n x p 矩阵。
通常对标准化数据应用 SVD。要将某个值标准化,需减去其均值,再除以其标准差。用 Xs 来表示标准化数据值的 n x p 矩阵。之后,标准化数据的协方差矩阵成为 X 的相关性矩阵,该矩阵定义如下:
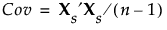
可以对 Xs 应用 SVD 来获取 Xs′Xs 的特征向量和特征值。当矩阵 X 很宽(很多列)或很高(很多行)时,这样做可以高效计算特征向量和特征值。此方法是宽 PCA 的基础。请参见““主成分”报表”。
逆协方差矩阵
一些多元方法需要计算协方差矩阵的逆矩阵。本节说明如何使用 SVD 来计算协方差矩阵的逆矩阵。
用 Xs 表示标准化数据矩阵并定义 S = Xs′Xs。奇异值分解允许您将 S 表示为:
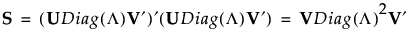
若 S 是满秩的,则 V 是 p x p 正交矩阵,您可以将 S-1 表示为:
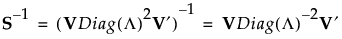
若 S 不是满秩的,则 Diag(L)-1 可以使用广义逆矩阵 Diag(L)+ 代替,其中 Diag(L) 的对角线元素用其倒数替代。这便按以下方式定义 S 的广义逆矩阵:
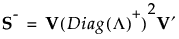
该广义逆矩阵只使用 SVD 就可以计算得到。
有关将 SVD 应用于宽线性判别分析的详细信息,请参见“宽线性判别方法”。
计算奇异值分解
在“多元方法”平台中,JMP 采用 Golub and Kahan (1965) 提出的方法计算矩阵的 SVD。Golub and Kahan 的方法是一个包含两个步骤的过程。第一步是将矩阵 M 简化为二对角矩阵 J。第二步是计算 J 的奇异值,它们与原始矩阵 M 的奇异值相同。通常将矩阵 M 的列标准化以便平衡变量对计算的影响。Golub and Kahan 方法的计算效率很高。