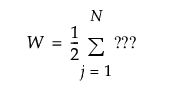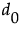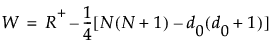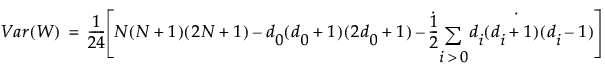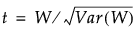Wilcoxon 检验允许存在结值。使用 Pratt 建议的方法,针对差值为 0 调整了检验统计量。请参见 Lehmann and D’Abrera (2006)、Pratt (1959) 和 Cureton (1967)。
|
•
|
有 N 个观测:
|
|
•
|
|
•
|
观测值与假设值 m 之间的差值计算如下:
|
|
•
|
有来自两个总体的 N 对观测:
|
|
•
|
|
•
|
|
•
|
R+ 是正符号秩的总和
对于 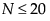 ,计算精确 p 值。
,计算精确 p 值。
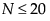 ,计算精确 p 值。
,计算精确 p 值。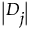 按最小到最大的顺序排列。
按最小到最大的顺序排列。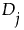 的秩或中秩。
的秩或中秩。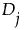 的符号秩定义如下:
的符号秩定义如下: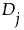 为正数,则符号秩为
为正数,则符号秩为 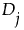 为 0,则符号秩为 0。
为 0,则符号秩为 0。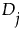 为负数,则符号秩为 -
为负数,则符号秩为 -