效应杠杆图亦称偏回归残差杠杆图 (Belsley et al. 1980) 或增加变量图 (Cook and Weisberg 1982)。Sall (1990) 推广了这些图,可应用于任何线性假设。
在效应杠杆图中,只有一个效应假定为 0。但在整体模型“预测值-实际值”图中,所有效应都假定为 0。Sall (1990) 发表的论文将杠杆图理念推广到了任意线性假设,整体模型杠杆图就是其中的一个例子。该论文中的详细信息(在本节中进行了总结)具体表示为 JMP 中的上述两类图。
|
•
|
|
•
|
vy 是水平轴值加上无约束残差
|
这些点构成杠杆图的基础。图 3.68对此构造进行了演示,其中,响应均值为 0,实线的斜率为 1。
图 3.68 杠杆图的构造
在简单线性回归中,您可以将响应期望值的置信限绘制为预测变量 x 的平滑函数
|
•
|
边界线 :若斜率参数的 t 检验恰好落在显著性边缘上,则置信曲线在响应均值处渐近水平线。
|
杠杆图通过显示置信曲线来体现这种思路。对这些曲线进行了调整以使图适当中心化。用 z 来表示水平轴上的点。定义函数
|
•
|
若 F 统计量大于参考值,则置信函数与水平轴交叉。
|
|
•
|
若 F 统计量等于参考值,则置信函数以水平轴为渐近线。
|
|
•
|
若 F 统计量小于参考值,则置信函数不交叉。
|
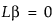
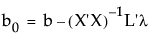
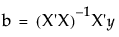
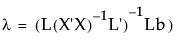
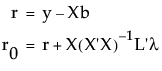
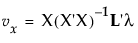 且
且 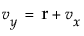
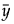 处有一条水平虚线。标绘的点的坐标为:(
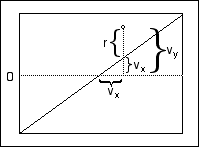
处有一条水平虚线。标绘的点的坐标为:(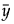 ,
, 
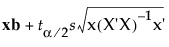
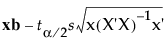
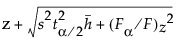
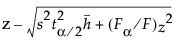
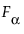 是显著性水平
是显著性水平 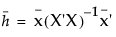 ,其中
,其中 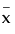 是由预测变量的合适中间值(如其均值)构成的行向量。
是由预测变量的合适中间值(如其均值)构成的行向量。