Bézier Curves

A complete discussion of Bézier curves is beyond the scope of this book. JSL has several commands for defining and drawing curves and their associated meshes.

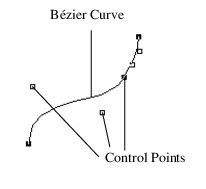
图 13.19 Bézier Curve

One-Dimensional Evaluators

To define a one-dimensional map, use the Map1 command.

Map1(target, u1, u2, stride, order, matrix)

The target argument defines what the control points represent. Values of the target argument are shown in Map1 Target Arguments and Default Values. Note that you must use the Enable command to enable the argument.

Map1 Target Arguments and Default Values
target Argument	Meaning
MAP1_VERTEX_3	(x, y, z) vertex coordinates
MAP1_VERTEX_4	(x, y, z, w) vertex coordinates
MAP1_INDEX	color index
MAP1_COLOR_4	R, G, B, A
MAP1_NORMAL	normal coordinates
MAP1_TEXTURE_COORD_1	s texture coordinates
MAP1_TEXTURE_COORD_2	s, t texture coordinates
MAP1_TEXTURE_COORD_3	s, t, r texture coordinates
MAP1_TEXTURE_COORD_4	s, t, r, q texture coordinates

The second two arguments (u1 and u2) define the range for the map. The stride value is the number of values in each block of storage (in other words, the offset between the beginning of one control point and the beginning of the next control point). The order should equal the degree of the curve plus one. The matrix holds the control points.

For example, Map1(MAP1_VERTEX_3, 0, 1, 3, 4, <4x3 matrix>) is typical for setting the two end points and two control points to define a Bézier line.

You use the MapGrid1 and EvalMesh1 commands to define and apply an evenly spaced mesh.

MapGrid1(un, u1, u2)

sets up the mesh with un divisions spanning the range u1 to u2. Code is simplified by using the range 0 to 1.

EvalMesh1(mode, i1, i2)

actually generates the mesh from i1 to i2. The mode can be either POINT or LINE. The EvalMesh1 command makes its own Begin and End clause.

The following example script demonstrates a one-dimensional outlier. A random set of control points draws a smooth curve. Only the first and last points are on the curve. Using NPOINTS=4 results in a cubic Bézier spline.

boxwide = 500;

boxhigh = 400;

gridsize = 100; // bigger for finer divisions

NPOINTS = 4;

/* We suggest you use only values between 2 and 8 (inclusively). Numbers beyond these might be interpreted differently, depending on implementation. This value is the degree+1 of the fitted curve */

point = J( NPOINTS, 3, 0 );

// create an array of x,y,z triples

For( x = 1, x <= NPOINTS, x++,

point[x, 1] = (x - 1) / (NPOINTS - 1) - .5;

// x from -.5 to +.5

point[x, 2] = Random Uniform() - .5;

// y is random in same range

point[x, 3] = 0;

// z is always zero, which causes the curve to stay in a plane

);

spline = Scene Box( boxwide, boxhigh );

spline << Ortho( -.6, .6, -.6, .6, -2, 2 );

// data from -.5 to .5 in x and y; this is a little larger

spline << Enable( MAP1_VERTEX_3 );

spline << MapGrid1( gridsize, 0, 1 );

spline << Color( .2, .2, 1 ); // blue curve

spline << Map1( MAP1_VERTEX_3, 0, 1, 3, NPOINTS, point );

spline << Line Width( 2 ); // not-so-skinny curve

spline << EvalMesh1( LINE, 0, gridsize ); // also try LINE, POINT

spline << Color( .2, 1, .2 );

spline << Point Size( 4 ); // big fat green points

// show the points and label them

For( i = 1, i <= NPOINTS, i++,

spline << Begin( "POINTS" );

spline << Vertex( point[i, 1], point[i, 2], point[i, 3] );

spline << End;

spline << Push Matrix;

spline << Translate( point[i, 1], point[i, 2], point[i, 3] );

spline << Text( center, bottom, .05, Char( i ) );

spline << Pop Matrix;

);

New Window( "Spline", spline );

https://www.tinaja.com/glib/bezconn.pdf offers an explanation of connecting cubic segments so that both the slope and the rate of change match at the connection point. This example does not illustrate doing so; there is only one segment here.