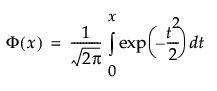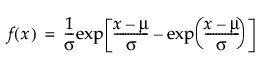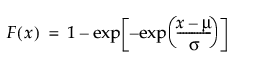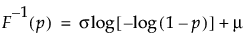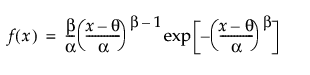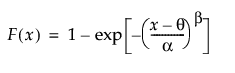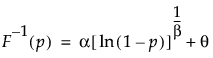Returns the probability density function (pdf) evaluated at x of the beta distribution. The pdf is parameterized as follows:
Optional scale parameter σ, which must be greater than 0. The default is 1.
Returns the cumulative distribution function (cdf) evaluated at x of the beta distribution. The cdf uses the same parameterization as the Beta Density() function.
Optional scale parameter σ, which must be greater than 0. The default is 1.
Returns the pth quantile from a beta distribution with shape arguments alpha and beta. The quantile function does not have a closed form equation.
The probability of the quantile desired; p must be between 0 and 1.
Optional scale parameter σ, which must be greater than 0. The default is 1.
Returns the probability density function (pdf) evaluated at q of a Cauchy distribution. The pdf is parameterized as follows:
Optional location parameter μ. The default is 0.
Optional scale parameter, σ, which must be greater than 0. The default is 1.
Returns the cumulative distribution function (cdf) probability that a Cauchy distributed random variable is less than q. The cdf is parameterized as follows:
Optional location parameter μ. The default is 0.
Optional scale parameter, σ, which must be greater than 0. The default is 1.
Returns the pth quantile from a Cauchy distribution. The pth quantile is the value for which the probability is p that a random value would be less than or equal to p. The quantile function is parameterized as follows:
The probability of the quantile desired; p must be between 0 and 1.
Optional location parameter μ. The default is 0.
Optional scale parameter σ, which must be greater than 0. The default is 1.
Returns the probability density function (pdf) evaluated at q of the chi-square distribution.
The degrees of freedom n, which must be greater than 0.
Optional non-centrality parameter λ, which must be non-negative. The default is 0.
Returns cumulative distribution function at quantile x for chi-square with df degrees of freedom centered at center.
The degrees of freedom, n, must be greater than 0.
The optional non-centrality parameter, λ, must be non-negative. The default is 0.
Returns the log of (1 - value), where value is the cumulative distribution function evaluated at x of the chi-square distribution with df degrees of freedom and non-centrality parameter nc.
Returns the log of the value of the probability density function evaluated at x of the chi-square distribution with df degrees of freedom and non-centrality parameter nc.
Returns the log of the value of the cumulative distribution function evaluated at quantile x of the chi-square distribution with df degrees of freedom and non-centrality parameter nc.
prob = ChiSquare Distribution(x, df, nc)
The degrees of freedom n, which must be greater than 0.
The probability of the quantile desired; prob must be between 0 and 1.
Returns the pth quantile from a chi-square distribution with df degrees of freedom, centered at nc. The quantile function does not have a closed form equation.
The probability of the quantile desired; p must be between 0 and 1.
The degrees of freedom n, which must be greater than 0.
Optional non-centrality parameter λ, which must be non-negative. The default is 0.
Returns the p-value from Dunnett’s multiple comparisons test.
A number that is the p-value.
Returns the probability density function (pdf) evaluated at x of the exponential distribution. The pdf is parameterized as follows:
A quantile at which the pdf is evaluated. x must be greater than or equal to 0.
Optional scale parameter θ, which must be greater than 0. The default is 1.
Returns the cumulative distribution function (cdf) evaluated at x of the exponential distribution. The cdf is parameterized as follows:
A quantile at which the cdf is evaluated. x must be greater than or equal to 0.
Optional scale parameter θ, which must be greater than 0. The default is 1.
Returns the pth quantile from an exponential distribution with scale parameter theta. The quantile function is parameterized as follows:
The probability of the quantile desired; p must be between 0 and 1.
Optional scale parameter θ, which must be greater than 0. The default is 1.
Returns the probability density function (pdf) evaluated at x for the F distribution with numerator and denominator degrees of freedom dfnum and dfden, with optional noncentrality parameter nc.
Returns cumulative distribution function (cdf) evaluated at x for the F distribution with numerator and denominator degrees of freedom dfnum and dfden and noncentrality parameter nc.
Returns the log of (1 - value), where value is the cumulative distribution function evaluated at x of the F distribution with numerator and denominator degrees of freedom dfnum and dfden, with optional noncentrality parameter nc.
Returns the log of the value of the probability density function (pdf) evaluated at x for the F distribution with numerator and denominator degrees of freedom dfnum and dfden, with optional noncentrality parameter nc.
Returns the log of the value of the cumulative distribution function (cdf) evaluated at x for the F distribution with numerator and denominator degrees of freedom dfnum and dfden and noncentrality parameter nc.
prob = F Distribution(x, dfn, dfd, nc)
Returns thepth quantile from the F distribution with numerator and denominator degrees of freedom dfnum and dfden and noncentrality parameter nc.
Returns the probability density function (pdf) evaluated at x of the Fréchet distribution. The pdf is parameterized as follows:
A number at which the pdf is evaluated. x must be greater than 0.
The scale parameter σ, which must be greater than 0.
Returns the cumulative distribution function (cdf) evaluated at x of the Fréchet distribution. The cdf is parameterized as follows:
A number at which the cdf is evaluated. x must be greater than 0.
The scale parameter σ, which must be greater than 0.
Returns the pth quantile from a Fréchet distribution with location mu and scale sigma. The quantile function is parameterized as follows:
The probability of the quantile desired; p must be between 0 and 1.
The scale parameter σ, which must be greater than 0.
Returns the probability density function (pdf) evaluated at x of the Gamma distribution. The pdf is parameterized as follows:
Optional shape parameter α, which must be greater than 0. The default is 1.
Optional scale parameter β, which must be greater than 0. The default is 1.
Returns the cumulative distribution function (cdf) evaluated at quantile x for the gamma distribution with parameters alpha, scale, and threshold.
Same as Log(1 – Gamma Distribution(x, alpha)) except that it has a much greater range.
Same as Log(Gamma Density(x, alpha)) except that it has a much greater range.
Same as Log(Gamma Distribution(x, alpha)) except that it has a much greater range.
Returns the pth quantile from the gamma distribution with the alpha, scale, and threshold parameters given.
Returns the probability density function (pdf) evaluated at x of an extended generalized gamma probability distribution. The pdf is parameterized as follows:
is the pdf for the standardized log-gamma variable and κ > 0 is a shape parameter.
A number at which the pdf is evaluated. x must be greater than 0.
The scale parameter σ, which must be greater than 0.
is the cdf for the standardized log-gamma variable and κ > 0 is a shape parameter.
A number at which the cdf is evaluated. x must be greater than 0.
The scale parameter σ, which must be greater than 0.
Returns the pth quantile from an extended generalized gamma distribution with parameters mu, sigma, and lambda. The quantile function does not have a closed form equation.
The probability of the quantile desired; p must be between 0 and 1.
The scale parameter σ, which must be greater than 0.
Returns the probability density function (pdf) evaluated at x of a generalized logarithmic distribution. The pdf is parameterized as follows:
The scale parameter σ, which must be greater than 0.
A shape parameter λ, which must be greater than 0.
Returns the probability that a generalized logarithmically distribution random variable is less than x.
Returns the probability density function (pdf) evaluated at q of a Johnson Sb distribution. The pdf is parameterized as follows:
Shape parameter γ that can be any value.
Shape parameter δ that must be greater than 0.
Location parameter θ that can be any value.
Scale parameter σ that must be greater than 0.
Returns the cumulative distribution function (cdf) evaluated at q of a Johnson Sb distribution. The pdf is parameterized as follows:
Shape parameter γ that can be any value.
Shape parameter δ that must be greater than 0.
Location parameter θ that can be any value.
Scale parameter σ that must be greater than 0.
Returns the pth quantile whose value for which the probability is p that a random value would be lower.
The probability of the quantile desired; p must be between 0 and 1.
Returns the probability density function (pdf) evaluated at x of a Johnson Sl distribution. The pdf is parameterized as follows:
Shape parameter γ that can be any value.
Shape parameter δ that must be greater than 0.
Location parameter θ that can be any value.
Parameter σ that defines if the distribution is skewed positively or negatively. Sigma must be equal to either +1 (skewed positively) or -1 (skewed negatively).
Returns the cumulative distribution function (cdf) evaluated at q of a Johnson Sl distribution.
A value that is in the interval theta to +infinity.
Parameter that defines if the distribution is skewed positively or negatively. Sigma must be equal to either +1 (skewed positively) or -1 (skewed negatively).
The probability of the quantile desired; p must be between 0 and 1.
Parameter that defines if the distribution is skewed positively or negatively. Sigma must be equal to either +1 (skewed positively) or -1 (skewed negatively).
Returns the probability density function (pdf) evaluated at x of a Johnson Su distribution. The pdf is parameterized as follows:
Shape parameter γ that can be any value.
Shape parameter δ that must be greater than 0.
Location parameter θ that can be any value.
Scale parameter σ that must be greater than 0.
Returns the cumulative distribution function (cdf) evaluated at q of a Johnson Su distribution. The cdf is parameterized as follows:
Shape parameter γ that can be any value.
Shape parameter δ that must be greater than 0.
Location parameter θ that can be any value.
Scale parameter σ that must be greater than 0.
Returns the pth quantile whose value for which the probability is p that a random value would be lower.
The probability of the quantile desired; p must be between 0 and 1.
Returns the probability density function (pdf) evaluated at x of the largest extreme value distribution with location mu and scale sigma. The pdf is parameterized as follows:
The scale parameter σ, must be greater than 0.
Returns the cumulative distribution function (cdf) evaluated at x of the largest extreme value distribution with location mu and scale sigma. The cdf is parameterized as follows:
The scale parameter σ, which must be greater than 0.
Returns the pth quantile from a largest extreme value distribution with location mu and scale sigma. The quantile function is parameterized as follows:
The probability of the quantile desired; p must be between 0 and 1.
The scale parameter σ, must be greater than 0.
Returns the probability density function (pdf) evaluated at x of a log generalized gamma probability distribution with parameters mu, sigma, and lambda. The pdf is parameterized as follows:
is the pdf for the log-gamma variable and κ > 0 is a shape parameter.
The scale parameter σ, which must be greater than 0.
Returns the cumulative distribution function (cdf) evaluated at x of the log generalized gamma distributed random variable (with parameters mu, sigma, and lambda) The cdf is parameterized as follows:
is the cdf for the log-gamma variable and κ > 0 is a shape parameter.
The scale parameter σ, which must be greater than 0.
Returns the pth quantile from a log generalized gamma distribution (with parameters mu, sigma, and lambda), the value for which the probability is p that a random variable would be lower.
Returns the probability density function (pdf) evaluated at x of a logistic distribution with location mu and scale sigma. The pdf is parameterized as follows:
The scale parameter σ, which must be greater than 0.
Returns the cumulative distribution function (cdf) evaluated at x of the logistic distribution with location mu and scale sigma. The cdf is parameterized as follows:
The scale parameter σ, which must be greater than 0.
Returns the pth quantile from a logistic distribution with location mu and scale sigma. The quantile function is parameterized as follows:
The probability of the quantile desired; p must be between 0 and 1.
The scale parameter σ, which must be greater than 0.
Returns the probability density function (pdf) evaluated at x of a loglogistic distribution with location mu and scale sigma. The pdf is parameterized as follows:
The scale parameter σ, which must be greater than 0.
Returns the cumulative distribution function (cdf) evaluated at x of the loglogistic distribution with location mu and scale sigma. The cdf is parameterized as follows:
The scale parameter σ, which must be greater than 0.
Returns the pth quantile from a loglogistic distribution with location mu and scale sigma. The quantile function is parameterized as follows:
The probability of the quantile desired; p must be between 0 and 1.
The scale parameter σ, which must be greater than 0.
Returns the probability density function (pdf) evaluated at x of a lognormal distribution with location mu and scale sigma. The pdf is parameterized as follows:
A number at which the pdf is evaluated. x must be greater than or equal to 0.
The scale parameter σ, which must be greater than 0.
Returns the cumulative distribution function (cdf) evaluated at x of a lognormal distribution with location mu and scale sigma. The cdf is parameterized as follows:
A number at which the pdf is evaluated. x must be greater than or equal to 0.
The scale parameter σ, which must be greater than 0.
Computes the probability that an observation (X, Y) is less than or equal to (x, y) with correlation coefficient r where X is individually normally distributed with mean mu1 and standard deviation s1 and Y is individually normally distributed with mean mu2 and standard deviation s2. If mu1, s1, mu2, and s2 are not given, the function assumes the standard normal bivariate distribution with mu1=0, s1=1, mu2=0, and s2=1.
Returns the probability density function (pdf) evaluated at x for the normal distribution with mean and stddev. The pdf is parameterized as follows:
Optional location parameter μ. The default is 0.
Optional scale parameter σ, which must be greater than 0. The default is 1.
Returns the cumulative distribution function (cdf) evaluated at x for the normal distribution with mean and stddev. The cdf is parameterized as follows:
Optional location parameter μ. The default is 0.
Optional scale parameter σ, which must be greater than 0. The default is 1.
Returns 1 - log (value) of the distribution function at quantile x for the normal distribution.
Returns the log of the value of the density function at quantile x for the normal distribution with mean and stddev. The default mean is 0. The default stddev is 1.
Returns the log of the value of the distribution function at quantile x for the normal distribution.
Returns the density at q of a normal mixture distribution with group means mean, group standard deviations stdev, and group probabilities probability. The mean, stdev, and probability arguments are all vectors of the same size.
Returns the probability that a normal mixture distributed variable with group means mean, group standard deviations stdev, and group probabilities probability is less than q. The mean, stdev, and probability arguments are all vectors of the same size.
Returns the pth quantile, the values for which the probability is p that a random value would be lower. The mean, stdev, and probability arguments are all vectors of the same size.
Returns the pth quantile from the normal distribution with mean and stddev. The default mean is 0. the default stddev is 1.
Returns the probability density function (pdf) evaluated at x of the smallest extreme distribution with location mu and scale sigma. The pdf is parameterized as follows:
The scale parameter σ, which must be greater than 0.
Returns the cumulative distribution function (cdf) evaluated at x of the smallest extreme distribution with location mu and scale sigma. The cdf is parameterized as follows:
The scale parameter σ, which must be greater than 0.
Returns the pth quantile of the smallest extreme distribution with location mu and scale sigma. The quantile function is parameterized as follows:
The probability of the quantile desired; p must be between 0 and 1.
The scale parameter σ, which must be greater than 0.
Returns the density at x of a sinh-arcsinh (SHASH) distribution.
Returns the value of the density function at quantile x for the Student’s t distribution with degrees of freedom df.
Returns the probability that a Student’s t distributed random variable is less than q. nonCentrality defaults to 0.
Returns the pth quantile from the Student’s t distribution with degrees of freedom df. nonCentrality defaults to 0.
Returns the p-value from Tukey’s HSD multiple comparisons test.
Returns the probability density function (pdf) evaluated at x of the Weibull distribution. The pdf is parameterized as follows:
Shape parameter β, which must be greater than 0.
Optional scale parameter α, which must be greater than 0. The default is 1.
Optional threshold parameter θ. The default is 0.
Returns the cumulative distribution function (cdf) at x of the Weibull distribution. The cdf is parameterized as follows:
Shape parameter β, which must be greater than 0.
Optional scale parameter α, which must be greater than 0. The default is 1.
Optional threshold parameter θ. The default is 0.
Returns the pth quantile from the Weibull distribution with the parameters given. The quantile function is calculated as follows:
The probability of the quantile desired; p must be between 0 and 1.
Shape parameter β, which must be greater than 0.
Optional scale parameter α, which must be greater than 0. The default is 1.
Optional threshold parameter θ. The default is 0.
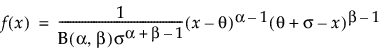 ,
,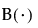 is the Beta function.
is the Beta function.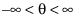 . The default is 0.
. The default is 0.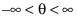 . The default is 0.
. The default is 0.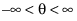 . The default is 0.
. The default is 0.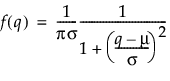
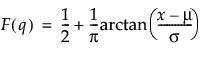
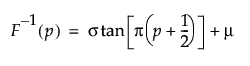
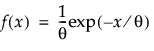
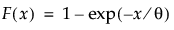
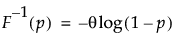
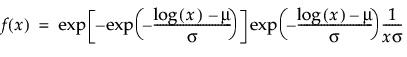
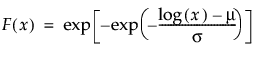
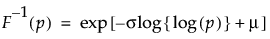
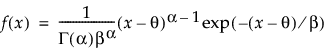
 . The default is 0.
. The default is 0.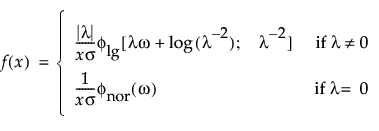
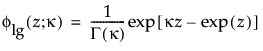
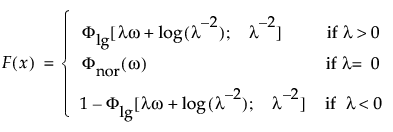
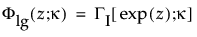
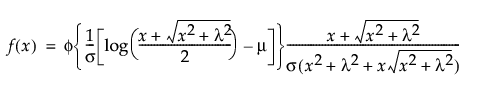
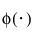 is the standard normal pdf.
is the standard normal pdf.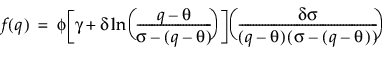
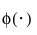 is the standard normal pdf.
is the standard normal pdf.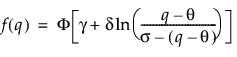
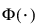 is the standard normal cdf.
is the standard normal cdf.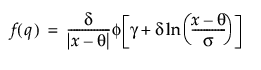
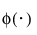 is the standard normal pdf.
is the standard normal pdf.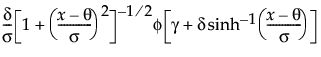
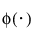 is the standard normal pdf.
is the standard normal pdf.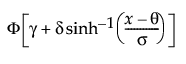
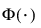 is the standard normal cdf.
is the standard normal cdf.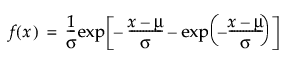
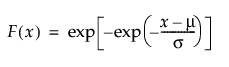
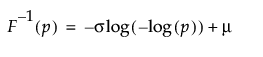
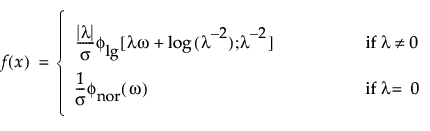
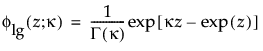
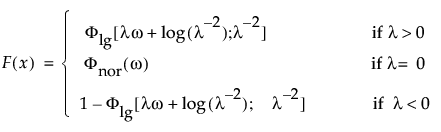
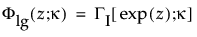
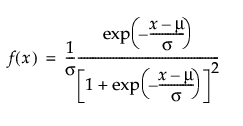
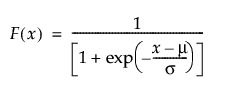
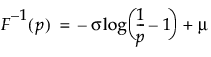
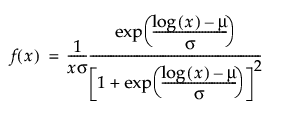
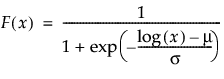
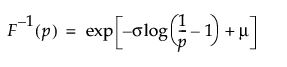
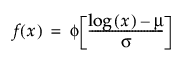
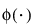 is the standard normal pdf.
is the standard normal pdf.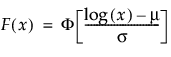
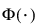 is the standard normal cdf.
is the standard normal cdf.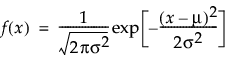
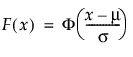
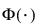 is the standard normal cdf, defined as follows:
is the standard normal cdf, defined as follows: