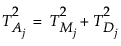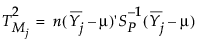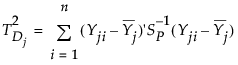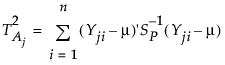考虑监控 p 个变量且获取大小为 n > 1 的 m 个子组的情况。为每个子组计算 T2 统计量并标绘它。T2 统计量和上控制限 (UCL) 的计算取决于目标统计量的来源。在“阶段 I”图中,限值基于在控制图上标绘的同一数据。在“阶段 II”图中,限值基于从历史数据集计算得出的目标统计量。有关 T2 统计量和 Hotelling T2 控制图的控制限计算的详细信息,请参见 Montgomery (2013)。
p = 变量数
n = 每个子组的样本大小
m = 子组数
p = 变量数
n = 子组样本大小
m = 历史数据集中的子组数
将 mn 个独立正态分布的观测样本分为 m 个大小为 n 的合理子组时,将 T2M 定义为第 j 个子组的均值 Y̅j 与目标值之间的间距。(对于合理子组中的观测,T2M 与上一节中的 T2 等价。)您还可以计算与每个子组中的内部变异性有关的 T2 统计量和围绕目标值的总变异性。T2 统计量的分量是可相加的,很像平方和。具体来说,以下关系对于 m 个子组均成立:
按以下方式定义与第 j 个子组的目标值的间距:
按以下方式定义第 j 个子组的内部变量性:
按以下方式定义第 j 个子组的总变异性:
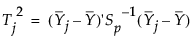
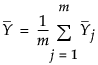
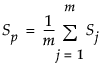 是合并的协方差矩阵,计算为子组内协方差矩阵的均值
是合并的协方差矩阵,计算为子组内协方差矩阵的均值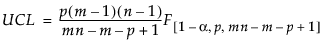
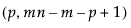
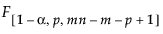 = (1–
= (1–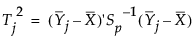
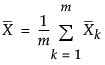
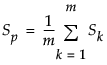 是合并的协方差矩阵,计算为子组内协方差矩阵的均值
是合并的协方差矩阵,计算为子组内协方差矩阵的均值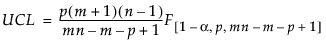
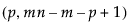
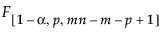 = (1–
= (1–