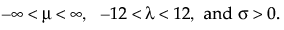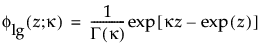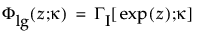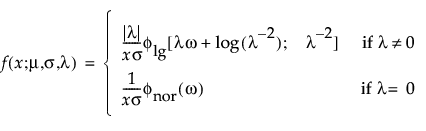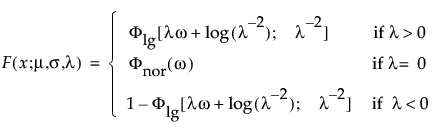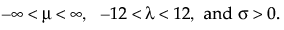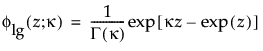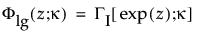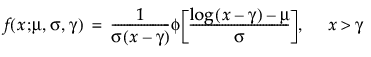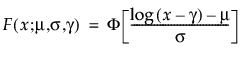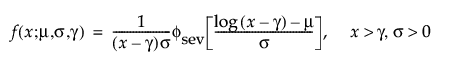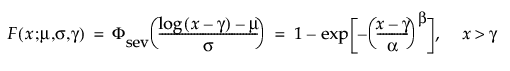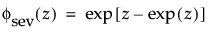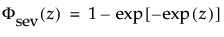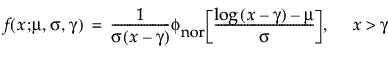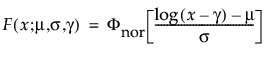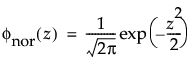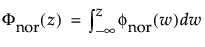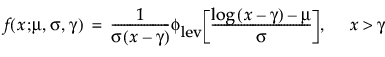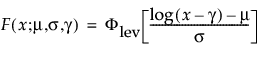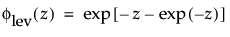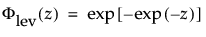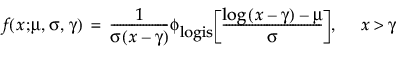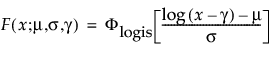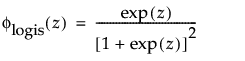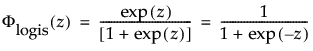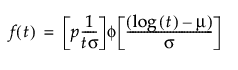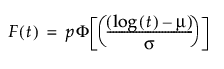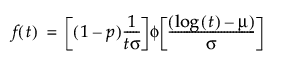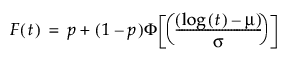本节提供有关“寿命分布”平台中的分布拟合的详细信息。Meeker and Escobar (1998, ch. 2-5) 是关于非参数和参数细节所依据的理论、应用和讨论的极佳信息来源。
所有分布的参数(除非另有说明)都使用最大似然估计值 (MLE) 来估计。唯一的例外是阈值分布。若最小的观测是一个精确失效,则该观测被视为具有小区间的区间删失。参数估计值是从这个稍作修改的数据集估计的 MLE。若不进行这项修改,似然会无界,所以 MLE 可能不存在。该方法类似于 Meeker and Escobar (1998, p. 275) 中所述的方法,只不过最小精确失效删失。这是为确保似然函数有界而对数据进行的最小更改。
“寿命分布”平台提供两种方法来计算分布参数的置信区间。这两种方法标记为“Wald”或“似然”,可在“寿命分布”平台的启动窗口中进行选择。Wald 置信区间用作默认设置。计算累积分布函数 (cdf) 的置信区间时,最初要计算标准化变量的 Wald 置信区间。接下来,这些区间变换为 cdf 尺度(Nelson, 1982, pp. 332–333 and pp. 346-347)。其他图形和刻画器中给出的置信区间变换为 Wald 区间 (Meeker and Escobar, 1998, chap. 7)。双参数分布的参数的联合置信区间显示在对数似然等高线图中。它们基于参数的近似似然比 (Meeker and Escobar, 1998, chap. 8)。
Weibull 分布可用于对具有递增或递减危险率的失效时间数据建模。由于该分布能够极为灵活地基于形状参数 β 的值对众多不同类型的数据建模,所以它经常用在可靠性分析中。 该分布已经成功用于描述电子元件、滚柱轴承、电容和陶瓷领域中的失效。可通过更改尺度参数 α 和形状参数 β 来显示 Weibull 分布的各种形状。 Weibull pdf 和 cdf 通常表示如下:
其中,α 是尺度参数,β 是形状参数。Weibull 分布极为通用,因为它可以在 β = 1 时简化为指数分布。在文献和 JMP 中常用的备选参数化是将 σ 用作尺度参数,将 μ 用作位置参数。这些参数很容易通过以下公式转换为 α 和 β 参数化:
正态分布是在多数统计领域中应用最广的分布,因为它相对简单并且易于应用中心极限定理。不过,正态分布极少用于可靠性领域。它对于 μ > 0 且变异系数 (σ/μ) 较小的数据最为有用。由于危险率函数增长没有上限,所以它尤其适用于显现出磨损失效的数据。示例包括白炽灯泡、烤箱加热元件和金属丝的机械强度。pdf 和 cdf 分别为:
这种非对称(左偏)分布适用于两种情况。第一种情况是数据指示少量的微弱单元位于分布的下尾处(该数据指示许多观测的最小数目)。第二种情况是在 σ 相对于 μ 较小时,因为在使用最小极值分布时小于零的概率较小。最小极值分布适用于描述危险率随单元老化而变大的数据。示例包括老年人死亡率和旱季的降雨量。该分布有时称为 Gumbel 分布。pdf 和 cdf 分别为:
其中,θ 是尺度参数,γ 既是阈值参数也是位置参数。可靠性分析常常使用单参数指数分布,其 γ = 0。指数分布适用于描述元件在远远超出期望寿命后显现出磨损的失效时间。该分布具有常数失效率,这意味着对于较小的时间增量,单元的失效与该单元龄无关。指数分布不应用于描述可能遭受疲劳、腐蚀或短期磨损的机械元件的寿命。但是,该分布适用于对特定类型的稳健电子元件建模。它已成功地被用来描述绝缘油和电介质流体的寿命 (Nelson, 1990, p. 53)。
分别为标准化对数 Gamma 变量的 pdf 和 cdf,并且 κ > 0 是形状参数。
阈值分布是带有阈值参数的对数-位置-尺度分布。上述有些分布通过添加阈值参数(表示为 γ)进行了推广。添加该阈值参数后,分布的左端点偏移了 0 点位置。阈值参数有时称为偏移、最小值或保证参数,因为所有单元都至少生存到阈值时间。请注意,尽管添加阈值参数使分布在时间轴上的位置发生偏移,但分布的形状和散布程度并不受影响。阈值分布适用于拟合中度到重度偏移的分布。对数-位置-尺度阈值分布的 pdf 和 cdf 的一般形式如下所示:
其中,φ 和 Φ 分别是特定分布的 pdf 和 cdf。针对 Weibull、对数正态、Fréchet 和对数 Logistic 分布的特定阈值分布的示例显示如下;其中相应地适当替换了最小极值、正态、最大极值和 logis 的 pdf 和 cdf。
p 是缺陷子总体分数
t 是寿命事件的测量时间
μ 和 σ 通过在从原始数据中删除零值后计算通常的最大似然估计来估计
若一定比例 (p) 的数据在 t = 0 时失效,就会使用零泛滥分布。当数据包含零的个数超出标准模型应有的个数时,就会造成零泛滥。在“寿命分布”平台中当事件时间数据以零作为最小值时,有四种零泛滥分布可用:这些分布包括:
p 是零数据值的比例
t 是寿命事件的测量时间
μ 和 σ 通过在从原始数据中删除零值后计算通常的最大似然估计来估计
有关可靠性分布的详细信息,请参见 Tobias and Trindade (1995, p. 232)。该参考文献提供了混合分布的一般形式。使用 Tobias and Trindade 中的参数化,可通过替换 α = p、Fd(t) = 1 和 FN(t) = Φ(t) 获得上述形式。
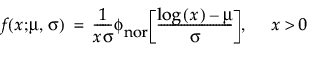
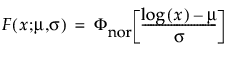 ,
,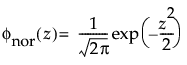
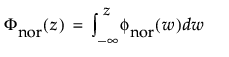
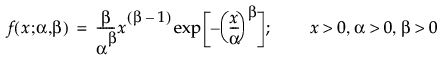
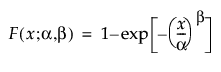 ,
,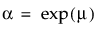
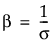
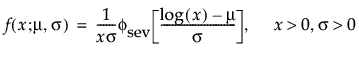

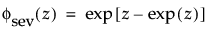
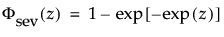
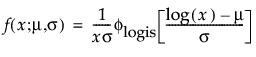
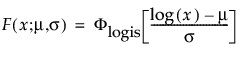 ,
,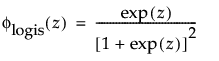
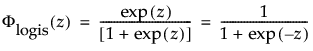
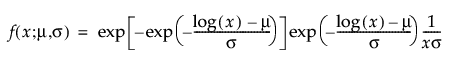
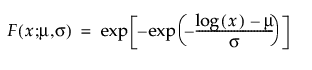
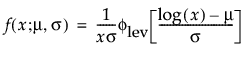
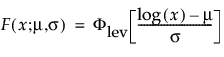
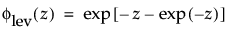
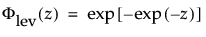
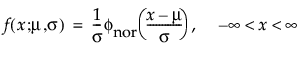
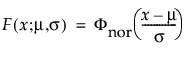
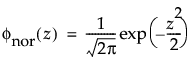
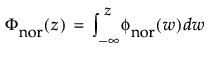
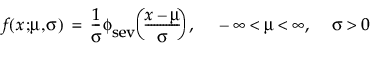
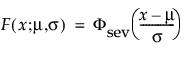
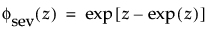
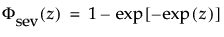
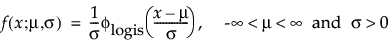
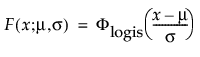
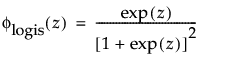
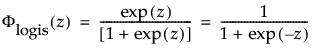
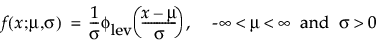
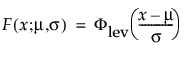
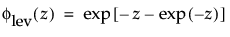
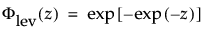
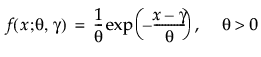 。
。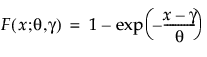
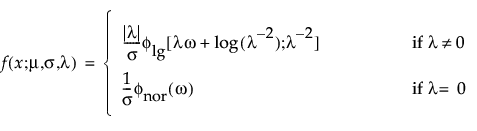
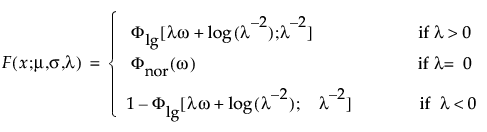
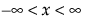 、
、