X 的效应杠杆图实际上是一个 X 残差对 Y 残差的散点图(整体模型和效应杠杆图)。为了帮助解释和比较您可能构造的其他图,JMP 向 Y 残差添加了 Y 均值,向 X 残差添加了 X 均值。转换的 Y 残差称为 Y 杠杆率残差,转换的 X 残差称为 X 杠杆率值。效应杠杆图上的点是这些 X 杠杆率与 Y 杠杆率残差配对而成的点。
一般杠杆图的演示显示如何在杠杆图中描述残差。从某个点到拟合线的距离是包含该效应的模型的残差。从该点到水平线的距离是模型中不含该效应时的剩余误差。换言之,杠杆图中的均值线表示参数(效应)的假设值被限制为 0 时的模型。
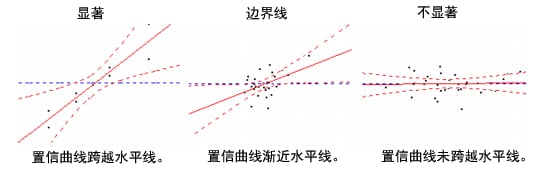
拟合线的置信曲线显示在杠杆图中。这些曲线直观地表明所关注的检验在 5% 水平下(或是您在“拟合模型”启动窗口中指定的“设置 Alpha 水平”下)是否显著。若曲线之间的置信区域包含表示假设的水平线,则效应不显著。若曲线跨越水平线,则效应显著。请参见比较杠杆图中显示的显著性中的示例。
若效应为名义型或有序型,或是效应是交互作用之类的复杂效应,则 x 轴无法直接表示效应值。在这种情况下,x 轴将按照响应的单位统一尺度,且拟合线是斜率为 1 的对角线。“整体模型”杠杆图(其中所关注的假设为“所有参数值均为 0”)使用该尺度。(请参见杠杆图详细信息。)对于该图,x 轴按照整体模型的预测响应值来统一尺度,如整体模型和效应杠杆图中的右图所示。
之所以使用杠杆率一词,是因为这些图可帮助您直观演示在模型中添加效应后各点对检验的影响。在水平方向距离图中心较远的点与接近中心的点相比,对效应检验发挥的影响更大。回想一下,效应检验涉及比较模型在包含和不含该效应时的残差平方和。在极值处,受假设约束之前和之后的残差的差值相对较大。因此,这些残差往往对该效应的假设检验的平方和有更大的贡献。
多重共线性是指这样一种状况:两个或更多预测变量高度相关,或从技术上更准确地说,涉及接近线性相关的关系。存在多重共线性时,标准误差可能会膨胀,参数估计值可能不稳定。若某个效应与其他预测变量共线,y 轴值会非常接近均值处的水平线,因为该效应没有带来任何新信息。由于这种相关,x 轴值也往往朝着图中央聚拢。这种情形指示拟合线的斜率不稳定。
“标绘效应杠杆图”选项为模型中的每个效应生成一个杠杆图。此外,“预测值-实际值”图也可被视为杠杆图。该图支持您直观演示关于模型中的所有参数(截距除外)均为 0 的检验。在“方差分析”报表中也会通过分析方法执行相同的检验。(有关该图的详细信息,请参见杠杆图详细信息。)
|
1.
|
|
2.
|
选择分析 > 拟合模型。
|
|
3.
|
|
4.
|
|
5.
|
点击运行。
|
整体模型“预测值-实际值”图以及针对身高的效应“杠杆图”显示在整体模型和效应杠杆图中。 左侧的整体模型图针对所有效应进行检验。您可以推断出该模型显著,因为置信曲线跨越响应体重均值处的水平线。右侧的身高“杠杆图”也显示身高是显著的,即便是模型中包含年龄和性别也是如此。这两个图均未表明需要担心与影响点或多重共线性相关的问题。