您可以创建一个公式，它计算 beta、卡方、F、gamma、正态、Student t、Weibull 分布、Tukey HSD 等统计分布的概率和分位数。有关语法的详细信息，请参见《JSL Syntax Reference》中的 Probability Functions。
接受标准正态分布的值范围的参数，它全部为实数。它返回参数的标准正态概率密度函数 (pdf) 的值。例如，您可以使用公式 count(-3, 3, nrow()) 创建一列值 (X)。在第二列中，插入公式 Normal Density(X) 以生成密度值。然后选择图形 > 图形生成器来按 X 绘制正态密度。
接受标准正态分布的值范围的参数 x，它全部为实数。它返回标准正态分布的观测值小于等于 x 的概率。例如，表达式 Normal Distribution(1.96) 返回 0.975，即标准正态分布的观测值小于等于分位数 1.96 的概率。还可以指定均值和标准差参数以获取非标准正态分布的概率。Normal Distribution 函数是 Normal Quantile 函数的反函数。
接受概率参数 p，并返回标准正态分布的第 p 分位数。例如，表达式 Normal Quantile(0.975) 返回标准正态分布的 97.5% 分位数，其求值结果为 1.96。还可以指定均值和标准差参数值以获取非标准正态分布的分位数。Normal Quantile 函数是 Normal Distribution 函数的反函数。
需要三个参数：分位数参数和形状参数 alpha 和 beta。阈值参数 (θ) 和尺度参数 (σ > 0) 是附加参数。它返回指定参数的 beta 概率密度函数 (pdf) 的值。beta 密度对于为随机变量的概率行为（如比例限制为落在区间 [0, 1]）建模很有用。
|
•
|
可选参数中心是分布的中位数。
|
|
•
|
可选参数尺度是四分位间距的一半，即，0.75 和 0.25 分位数之差的一半。
|
接受参数 x（可以为任意实数）以及可选参数中心和尺度。若您未指定可选参数的值，则函数返回具有中位数为 0 和第三四分位数为 1 的分布的 Cauchy 累积分布函数 (cdf) 在 x 处的值。若您指定了中心和尺度的值，则函数返回具有中位数（由中心给定）和四分位间距（由尺度的两倍给定）的 Cauchy 分布的累积分布函数在 x 处的值。
接受参数 prob（可以为 0 和 1 之间的任意数字）和可选参数中心和尺度。若您未指定可选参数的值，函数返回具有中位数为 0 和第三四分位数为 1 的 Cauchy 分布的第 p 分位数（其中 p = prob）。若您指定了中心和尺度的值，则函数返回具有中位数（由中心给定）和四分位间距（由尺度的两倍给定）的 Cauchy 分布的第 p 分位数。
接受响应参数（x 值的范围）和三个参数：分位数、自由度和非中心参数。它返回具有指定非中心参数和自由度的卡方分布的观测值小于等于指定分位数的概率。例如，表达式 ChiSquare Distribution(11.264, 5) 返回中心为 0、自由度为 5 的卡方分布的观测值小于等于 11.264 的概率。表达式的求值结果为 0.95361。
此外，ChiSquare Distribution 函数接受整数和非整数自由度。默认中心为 0。ChiSquare Distribution 函数是 ChiSquare Quantile 函数的反函数。
接受三个参数：概率 p、自由度和非中心参数。它从具有指定非中心参数和自由度的卡方分布返回第 p 分位数。例如，表达式 ChiSquare Quantile(.95, 3.5, 4.5) 从中心为 4.5、自由度为 3.5 的卡方分布返回 95% 分位数。表达式求值结果为 17.50458。
返回 Dunnett 的多重比较检验中的 p 值。
接受四个参数：分位数、分子和分母自由度参数以及非中心参数。它返回具有指定非中心参数和自由度的 F 分布的观测值小于等于指定分位数的概率。例如，表达式 F Distribution(3.32, 2, 3) 返回分子自由度为 2、分母自由度为 3 的中心 F 分布的观测值小于等于 3.32 的概率。表达式求值结果为 0.82639。
返回 1 - F 分布的对数。
返回 F 分布的对数。
求解非中心参数，使得 prob=F-distribution (x, ndf, ddf, nc)。
F Power 函数计算涉及 F 检验或 t 检验的指定情形的功效，F Sample Size 函数则计算样本大小。参数是为前瞻功效分析计算指定的值。（这些函数执行与您选择实验设计 > 样本大小与功效相同的计算。有关功效和样本大小的讨论，请参见《实验设计指南》中的前瞻样本大小与功效。）这些参数包括：
|
•
|
alpha 您可以接受的显著性水平（通常为 0.05）。
|
|
•
|
dfh 假设自由度。对于 t 检验，它的值为 1。
|
|
•
|
|
•
|
将 
用于单样本 t 检验
用于单样本 t 检验将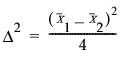 
用于双样本 t 检验
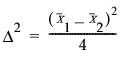用于双样本 t 检验
用于 |
•
|
接受四个参数：概率 p、分子和分母自由度以及非中心参数。它从具有指定非中心参数和自由度的 F 分布返回第 p 分位数。例如，表达式 F Quantile(0.95, 2, 10, 0) 从中心为 0、分子自由度为 2 和分母自由度为 10 的 F 分布返回 95% 分位数。表达式求值结果为 4.1028。
需要分位数参数。还接受可选的 alpha 形状参数，该参数必须大于 0，默认为 1。尺度参数 b 是可选的，它必须大于 0，默认为 1。阈值参数是可选的，它必须位于范围 -∞ < θ < +∞ 内，默认为 0。
Gamma Density 示例显示 gamma 概率密度函数在形状参数为 1、3 和 5 时的形状。标准 gamma 密度函数在 α (形状) ≤1 时严格递减。当 α > 1，密度函数从 0 开始，当 x 为 θ 时，增加到最大值，然后递减。
基于标准 gamma 函数，接受带分位数值的单个参数。形状、尺度和阈值参数是可选的，其默认值如前面 Gamma Density 函数中所述。它返回标准 gamma 分布的观测值小于等于指定的 x 的概率。Gamma Distribution 函数是 Gamma Quantile 函数的反函数。
返回广义 Gamma 分布的分位数，其随机值小于该值的概率为 p。mu、sigma 和 lambda 分别为参数。
返回 Johnson Sb 分布的随机变量小于等于 x 的概率。有四个可选参数：gamma、delta、theta 和 sigma。有关 Johnson Sb 分布和这些参数的说明，请参见《JSL Syntax Reference》手册中的 Johnson Sb Distribution(q, gamma, delta, theta, sigma)。
返回 Johnson Sb 分布的第 p 分位数。有四个可选参数：gamma、delta、theta 和 sigma。有关 Johnson Sb 分布和这些参数的说明，请参见《JSL Syntax Reference》手册中的 Johnson Sb Quantile(p, gamma, delta, theta, sigma)。
返回 Johnson Sb 分布在 x 处的密度。有四个可选参数：gamma、delta、theta 和 sigma。有关 Johnson Sb 分布和这些参数的说明，请参见《JSL Syntax Reference》手册中的 Johnson Sl Density(q, gamma, delta, theta, sigma)。
返回 Johnson Sl 分布的随机变量小于等于 x 的概率。有四个可选参数：gamma、delta、theta 和 sigma。有关 Johnson S1 分布和这些参数的说明，请参见《JSL Syntax Reference》手册中的 Johnson Sl Distribution(q, gamma, delta, theta, sigma)。
返回 Johnson Sl 分布的第 p 分位数。有四个可选参数：gamma、delta、theta 和 sigma。有关 Johnson S1 分布和这些参数的说明，请参见《JSL Syntax Reference》手册中的 Johnson Sl Quantile(p, gamma, delta, theta, sigma)。
返回 Johnson Sl 分布在 x 处的密度。有四个可选参数：gamma、delta、theta 和 sigma。有关 Johnson S1 分布和这些参数的说明，请参见《JSL Syntax Reference》手册中的 Johnson Sl Density(q, gamma, delta, theta, sigma)。
返回 Johnson Su 分布的随机变量小于等于 x 的概率。有四个可选参数：gamma、delta、theta 和 sigma。有关 Johnson Su 分布和这些参数的说明，请参见《JSL Syntax Reference》手册中的 Johnson Su Distribution(q, gamma, delta, theta, sigma)。
返回 Johnson Su 分布的第 p 分位数。有四个可选参数：gamma、delta、theta 和 sigma。有关 Johnson Su 分布和这些参数的说明，请参见《JSL Syntax Reference》手册中的 Johnson Su Quantile(p, gamma, delta, theta, sigma)。
返回 Johnson Su 分布在 x 处的密度。有四个可选参数：gamma、delta、theta 和 sigma。有关 Johnson Su 分布和这些参数的说明，请参见《JSL Syntax Reference》手册中的 Johnson Su Density(q, gamma, delta, theta, sigma)。
返回对数广义 Gamma 分布的分位数，其随机值小于该值的概率为 p。mu、sigma 和 lambda 分别为参数。
接受 t 分布的值范围的分位数参数、自由度参数和可选的非中心参数。它返回参数的 t 密度函数 (pdf) 的值。为了比较自由度为 5 的 t 密度与标准正态分布，您可以使用公式 count(-3, 3, nrow()) 创建一列分位数值 (X)。在第二列中插入公式 t Density(X, 5)。在第三列中插入公式 Normal Density(X)。然后选择图形 > 图形生成器来按 X 绘制 t 密度和正态密度。您将看到 t 密度比正态密度略为分散一些。
接受三个参数：分位数、自由度和非中心参数。它返回具有指定非中心参数和自由度的 Student t 分布观测值小于等于指定分位数的概率。例如，表达式 t Distribution(.9, 5) 返回中心为 0、自由度为 5 的 Student t 分布观测值小于等于 0.9 的概率。表达式求值结果为 0.79531。t 分布接受整数和非整数自由度。默认情况下，它的中心为 0，但是您可以输入非中心参数的值。t Quantile 函数是 t Distribution 函数的反函数。
求解非中心参数，使得 prob=T Distribution (x, df, nc)。
接受三个参数：概率 p、自由度和非中心参数。它从具有指定非中心参数和自由度的 Student t 分布返回第 p 分位数。例如，表达式 Student's t Quantile(.95, 2.5) 从中心为 0、自由度为 2.5 的 Student t 分布返回 95% 分位数。表达式求值结果为 2.558219。t Quantile 函数是 t Distribution 函数的反函数。该函数还接受整数和非整数自由度。默认情况下，它的中心为 0，但是您可以通过选项输入非中心参数的值。t Distribution 函数是 t Quantile 函数的反函数。
接受概率参数 1-alpha，并从指定参数的 Tukey HSD 检验返回 1-alphath 分位数。alpha 参数是您指定的显著性水平。nGroups 是某一研究的组数。dfe 是误差自由度（基于总研究样本）。这是用在 Tukey 的多重比较检验中计算最小显著性差异的分位数。
返回 Tukey HSD 多重比较检验的 p 值。
接受来自 Weibull 分布的值范围的分位数参数，以及可选形状、尺度和阈值参数。具有形状参数 β、尺度参数 α 和阈值参数 θ 的 Weibull 分布的密度函数在《基本分析》手册的Weibull、有阈值的 Weibull 和极值中给出。Weibull Density 函数返回对应 Weibull 分布的概率密度函数 (pdf) 的值。
接受来自 Weibull 分布的值范围的分位数参数 x，以及可选形状、尺度和阈值参数。具有形状参数 β、尺度参数 α 和阈值参数 θ 的 Weibull 分布的分布函数在《基本分析》手册中给出。Weibull Distribution 函数返回具有指定形状、尺度和阈值参数的 Weibull 分布的观测值小于等于指定 x 的概率。Weibull Distribution 函数是 Weibull Quantile 函数的反函数。
Weibull 分布根据不同的 α（影响 x 方向的尺度参数）值和 β（形状参数）值而具有不同的形状。它通常为估计寿命（特别是机械设备和生物方面）提供合适的模型。双参数的 Weibull 和阈值为零的三参数 Weibull 相同。