The Model Summary table contains fit statistics for the model. In the formulas below, n is the length of the series and k is the number of fitted parameters in the model.
The unconditional sum of squares (SSE) divided by the number of degrees of freedom (n – k). The variance estimate is computed as SSE / (n – k). This is the sample estimate of the variance of the random shocks at, described in the section ARIMA Model.
If the model does not fit the series well, the model error sum of squares, SSE, might be larger than the total sum of squares, SST. As a result, R2 can be negative.
Twice the negative log-likelihood function evaluated at the best-fit parameter estimates. Smaller values are better fits. See Likelihood, AICc, and BIC in the Fitting Linear Models book.
Indicates whether the moving average operator is invertible. That is, whether all the roots of 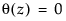 lie outside the unit circle.
lie outside the unit circle.
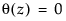 lie outside the unit circle.
lie outside the unit circle.The name of the parameter, which are described in the sections for each model type. Some models contain an intercept or mean term. In those models, the related constant estimate is also shown. The definition of the constant estimate is given under the description of ARIMA models.
The test statistics for the hypotheses that each parameter is zero. The test statistic for a parameter is the ratio of the parameter estimate to its standard error. If the hypothesis is true, then this statistic has an approximate Student’s t distribution. Looking for a t-ratio greater than 2 in absolute value is a common rule for judging significance because it approximates the 0.05 significance level.
The observed p-value calculated for each parameter. The p-value is the probability of getting, by chance alone, a t-ratio greater (in absolute value) than the computed value, given a true hypothesis.
Controls the displays of residual statistics are shown for the model. These displays are described in the section Time Series Platform Options. However, they are applied to the series of residuals.





 are the one-step-ahead forecasts
are the one-step-ahead forecasts is the mean
is the mean 


 lie outside the unit circle.
lie outside the unit circle.