Consider first the case of a single parameter, θ. Let l be the log-likelihood function for θ and let x be the data. The score is the derivative of the log-likelihood function with respect to θ:
The score test can be generalized to multiple parameters. Consider the vector of parameters θ. Then the test statistic for the score test of H0: 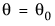 is:
is:
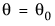 is:
is:The test statistic is asymptotically Chi-square distribution with k degrees of freedom. Here k is the number of unbounded parameters.
Let 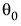 be the value of
be the value of  where the algorithm terminates. Note that the relative gradient evaluated at
where the algorithm terminates. Note that the relative gradient evaluated at 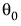 is the score test statistic. A p-value is calculated using a Chi-square distribution with k degrees of freedom. This p-value gives an indication of whether the value of the unknown MLE is consistent with
is the score test statistic. A p-value is calculated using a Chi-square distribution with k degrees of freedom. This p-value gives an indication of whether the value of the unknown MLE is consistent with  . The number of unbounded parameters listed in the Random Effects Covariance Parameter Estimates report equals k.
. The number of unbounded parameters listed in the Random Effects Covariance Parameter Estimates report equals k.
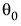 be the value of
be the value of  where the algorithm terminates. Note that the relative gradient evaluated at
where the algorithm terminates. Note that the relative gradient evaluated at 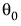 is the score test statistic. A p-value is calculated using a Chi-square distribution with k degrees of freedom. This p-value gives an indication of whether the value of the unknown MLE is consistent with
is the score test statistic. A p-value is calculated using a Chi-square distribution with k degrees of freedom. This p-value gives an indication of whether the value of the unknown MLE is consistent with  . The number of unbounded parameters listed in the Random Effects Covariance Parameter Estimates report equals k.
. The number of unbounded parameters listed in the Random Effects Covariance Parameter Estimates report equals k. Convergence Score Test
Convergence Score Test Score Test
Score Test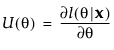

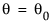 is:
is:


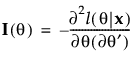
 denotes the transpose of the matrix
denotes the transpose of the matrix  Relative Gradient
Relative Gradient . Here,
. Here,  is the gradient of the log-likelihood function and
is the gradient of the log-likelihood function and  is its Hessian.
is its Hessian.