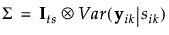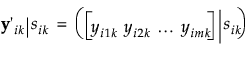The form of the repeated measures model is yijk = αij + sik + eijk, where

Assume that the sik are independent and identically distributed N(0, σs2) variables. Denote the number of treatment factors by t and the number of subjects by s. Then the distribution of eijk is N(0, Σ), where

Denote the block diagonal component of the covariance matrix Σ corresponding to the ikth subject within treatment by Σik. In other words, Σik = Var(yik|sik). Because observations over time within a subject are not typically independent, it is necessary to estimate the variance of yijk|sik. Failure to account for the correlation leads to distorted inference.

See Repeated Covariance Structures and Spatial and Temporal Variability for more information about the covariance structures available for Σik.