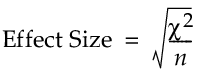Multivariate Methods • Latent Class Analysis • The Latent Class Analysis Report
Previous
 • 
Next
The Latent Class Analysis Report
The initial Latent Class Analysis report contains a Cluster Comparison and Latent Class Model reports for each specified number of clusters.
Cluster Comparison Report
The Cluster Comparison report gives fit statistics to compare the various models. The fit statistics are the negative log-likelihood (-LogLikelihood), BIC, and AIC. Smaller values of each indicate better fit. The best fit is indicated in a column called Best.
Latent Class Model for <k> Clusters Report
The Latent Class Model Report for <k> Clusters contains the following results and outlines:
•
Model Summary
•
Parameter Estimates
•
Transposed Parameter Estimates
•
Effect Sizes
•
MDS Plot
•
Mixture Probabilities
Model Summary
By default, a summary of the model for the specified number of clusters appears at the top of each Latent Class Model report. The model summary contains the -LogLikelihood, Number of Parameters, BIC, and AIC. These summary values can be used to determine how well the model fits the data. Lower values of -LogLikelihood, BIC, and AIC indicate better fits. For more information, see Likelihood, AICc, and BIC in the Fitting Linear Models book. The Number of Parameters value gives the number of unique parameters in the latent class model. For more information, see Statistical Details for the Latent Class Analysis Platform.
Parameter Estimates
The Parameter Estimates report contains tabular and graphical summaries of the parameter estimates and is displayed by default. Each summary contains rows corresponding to the model clusters.
The Overall column shows the probability of an observation belonging to each cluster. (These are the γ parameters. See Statistical Details for the Latent Class Analysis Platform.)
The remaining columns in the displays are grouped with vertical dividers according to the Y columns specified in the Latent Class Analysis launch window:
•
Each group of categorical response columns has a column for each level within the respective response. In each group, the value in a given row and column is the conditional probability of the response indicated by the column, given that the observation belongs to the cluster identified by the row. (These are the ρ parameters.)
•
Each group of multiple response columns has a column for each category within the multiple response. In each group, the value in a given row and column is the conditional probability of a response at the lower level of the indicated category, given that the observation belongs to the cluster identified by the row. (These are the ρ parameters.)
The graphical display shows the conditional probability values as share charts. For each cluster and each Y, the conditional probabilities given cluster membership are plotted as a horizontal stacked bar chart. For a binary or nominal response column, the percentages in these charts sum to one for each response. For a multiple response column, the percentages are of the lower level of each of the categories and do not sum to one. The stacking of bars follows the order of appearance of the variables in the table of values. You can also place your cursor over the bars to view the levels or categories of the variable.
Tip: You can select one or more rows in either table in the Parameter Estimates report to select the observations assigned to the corresponding clusters.
Transposed Parameter Estimates
The Transposed Parameter Estimates report contains a table that is the transpose of the Parameter Estimates report table. Here the clusters are shown as columns. The conditional probabilities for each cluster are shown for each response category of each Y column in the analysis.
Note: The estimates from the Overall column are not included in the transposed table.
Effect Sizes
The Effect Sizes table compares the Y columns across clusters and is displayed by default. The statistics in each row of this table are obtained from a contingency table analysis of expected counts for cluster membership by levels or categories of a Y column. The expected counts are obtained by multiplying the number of observations in each cluster by the conditional probabilities for each level or category of the Y column.
For each response, the Pearson chi-square statistic, χ 2, is calculated for the contingency table of expected counts for levels by clusters. Let n represent the number of observations. The value in the Effect Size column is defined as follows:
Each value in the LR Logworth column shows -log10(pLR) where pLR is the likelihood ratio test p-value for the contingency table of expected counts. A Logworth value above 2 corresponds to significance at the 0.01 significance level.
Tip: You can select one or more rows in the Effect Sizes table to select the corresponding columns in the data table.
MDS Plot
The MDS Plot contains one point for each cluster and is displayed by default. It is a two-dimensional representation of cluster proximity. Clusters that are closer together are more similar. The plot is created from a dissimilarity matrix of the ρ parameters. For more information about MDS plots, see the Multidimensional Scaling topic.
Mixture Probabilities
The Mixture Probabilities table displays probabilities of cluster membership for each row. The Most Likely Cluster column indicates the cluster with the highest probability of membership for each row.
Note: Rows that contain a missing value for one or more of the Y columns are excluded from the analysis and do not appear in the Mixture Probabilities table.

Previous
 • 
Next
Help created on 7/12/2018