Verteilung von stetigen Variablen
Das Analysieren einer stetigen Variablen kann Fragestellungen etwa nach der Form der Verteilung und dem Durchschnitt der Daten beinhalten.
• Passt die Form der Daten zu bekannten Verteilungen?
• Enthalten die Daten Ausreißer?
• Wie ist der Durchschnittswert der Daten?
• Unterscheidet sich der Durchschnittswert statistisch von einem Ziel oder historischen Wert?
• Wie verteilt sind die Daten? Anders gefragt: Wie ist die Standardabweichung?
• Welches sind die Mindest- und Höchstwerte?
Sie können diese und andere Fragen mit Graphen, zusammenfassenden Statistiken und einfachen statistischen Tests beantworten.
Szenario
In diesem Beispiel wird die Datentabelle Car Physical Data.jmp verwendet, die Informationen über 116 verschiedene Automodelle enthält.
Ein Planungsexperte wurde von einem Bahnunternehmen ersucht, die möglichen Probleme beim Transport von Autos per Bahn zu ermitteln. Anhand der Daten möchte der Experte folgende Fragestellungen behandeln:
• Wie hoch ist das durchschnittliche Autogewicht?
• Wie verteilt sind die Gewichte des Autos (Standardabweichung)?
• Welches sind die Mindst- und Höchstgewichte der Autos?
• Enthalten die Daten Ausreißer?
Verwenden Sie ein Histogramm der Gewichte, um diese Fragen zu beantworten.
Histogramm erstellen
1. Wählen Sie Hilfe > Beispieldatenordner und öffnen Sie Car Physical Data.jmp.
2. Wählen Sie Analysieren > Verteilung aus.
3. Wählen Sie Weight aus und klicken Sie auf Y, Spalten.
4. Klicken Sie auf OK.
5. Um das Berichtsfenster zu drehen, klicken Sie auf das rote Dreieck „Weight“ und wählen Anzeigeoptionen > Horizontales Layout aus.
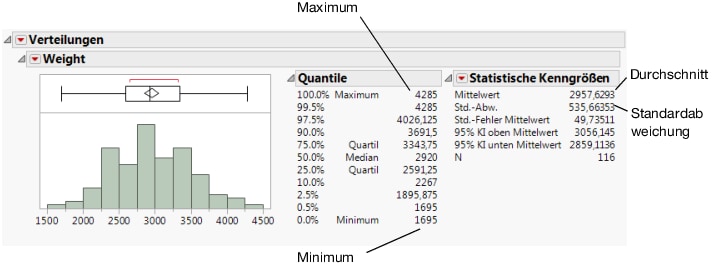
Abbildung 5.7 Verteilung des Wertes Weight
Das Berichtsfenster ist in drei Abschnitte unterteilt:
• Ein Histogramm und ein Box-Plot zur Visualisierung der Daten.
• Ein Quantile-Bericht, der die Perzentile der Verteilung zeigt.
• Ein Bericht über statistische Kennzahlen, der Mittelwert, Standardabweichung und andere Statistiken anzeigt.
Verteilungsergebnisse interpretieren
Unter Verwendung der Ergebnisse in Abbildung 5.7 kann der Planungsexperte die Fragen beantworten.
Wie hoch ist das durchschnittliche Autogewicht?
Das Histogramm zeigt ein durchschnittliches Gewicht von ca. 3.000 lbs.
Wie sind die Gewichte verteilt (Standardabweichung)?
Die statistischen Kenngrößen zeigen ein durchschnittliches Gewicht von ca. 2.958 lbs. Die statistischen Kenngrößen zeigen eine Standardabweichung von ca. 536 lbs.
Welches sind die Mindest- und Höchstgewichte?
Das Histogramm zeigt ein Minimum von ca. 1.500 lbs. und ein Maximum von ca. 4.500 lbs. Im Bereich Quantile werden als Minimum ca. 1.695 lbs. und als Maximum ca. 4.285 lbs. genannt.
Gibt es Ausreißer?
Nein.
Das Standard-Berichtsfenster in Abbildung 5.7 zeigt eine Mindestmenge von Graphen und Statistiken. Zusätzliche Graphen und Statistiken sind im roten Dreiecksmenü verfügbar.
Schlussfolgerungen ziehen
Basierend auf anderen Studienergebnissen hat das Bahnunternehmen festgestellt, dass ein Durchschnittsgewicht von 3000 Pfund das effizienteste Transportgewicht darstellt. Jetzt muss der Planungsexperte herausfinden, ob das durchschnittliche Autogewicht in der allgemeinen Population der untersuchten Autos, die vom Bahnunternehmen transportiert werden können, 3000 Pfund beträgt. Verwenden Sie einen t-Test, um Schlüsse über die zugrunde liegende Grundgesamtheit basierend auf dieser Stichprobe zu ziehen.
Schlussfolgerungen testen
1. Klicken Sie auf das rote Dreieck „Weight“ und wählen Sie Test Mittelwert aus.
2. In dem nun eingeblendeten Fenster geben Sie in das Feld „Geben Sie den hypothetischen Mittelwert ein“ den Wert 3000 ein.
3. Klicken Sie auf OK.
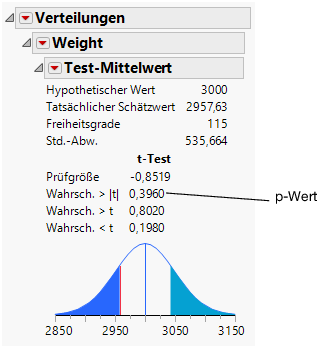
Abbildung 5.8 Testen der Mittelwertergebnisse
T-Test interpretieren
Das primäre Ergebnis eines t-Tests ist der p-Wert. In diesem Beispiel ist der p-Wert 0,396 und der Analyst verwendet ein Signifikanzniveau von 0,05. Da 0,396 größer als 0,05 ist, können Sie daraus nicht den Schluss ziehen, dass das Durchschnittsgewicht von Automodellen in der breiteren Bevölkerung signifikant von 3000 Pfund abweicht. Wäre der p-Wert niedriger gewesen als das Signifikanzniveau, hätte der Experte daraus geschlossen, dass das durchschnittliche Autogewicht in der Grundgesamtheit tatsächlich signifikant von 3000 Pfund abweicht.