Example of a Reliability Growth Model with Interval-Censored Data
This example fits a piecewise NHPP Weibull model with interval-censored data. The data are failures for a turbine engine design over three phases of a testing program. The first two columns give time intervals during which failures occurred. These intervals are recorded as days since the start of testing. The exact failure times are not known; it is known only that failures occurred within these intervals.
The reports of failures are provided generally at weekly intervals. Intervals during which there were no failures and which fell strictly within a phase are not included in the data table (for example, the interval 106 to 112 is not represented in the table). Because these make no contribution to the likelihood function, they are not needed for estimation of model parameters.
However, to fit a Piecewise Weibull NHPP or Reinitialized Weibull NHPP model, it is important that the start times for all phases be provided in the Time to Event or Timestamp columns.
Here, the three phases began at days 0 (Initial phase), 91 (Revised phase), and 200 (Final phase). There were failures during the weeks that began the Initial and Revised phases. However, no failures were reported between days 196 and 231. For this reason, an interval with beginning and ending days equal to 200 was included in the table (row 23), reflecting 0 failures. This is necessary to determine the start time of the Final phase.
The test was terminated at 385 days. This is an example of interval-censored failure times with time terminated phases.
Note: The phase start times are required for proper display of the transition times for the Piecewise Weibull NHPP model; they are required for estimation of the Reinitialized Weibull NHPP model. For interval-censored data, the algorithm defines the beginning time for a phase as the start date recorded in the row containing the first occurrence of that phase designation. In this example, if row 23 were not in the table, the beginning time of the Final phase would be taken as 231.
1. Select Help > Sample Data Folder and open Reliability/TurbineEngineDesign2.jmp.
2. Select Analyze > Reliability and Survival > Reliability Growth.
3. On the Time to Event Format tab, select the columns Interval Start and Interval End, and click Time to Event.
4. Select Fixes and click Event Count.
5. Select Design Phase and click Phase.
6. Click OK.
7. Click the Reliability Growth red triangle and select Fit Model > Piecewise Weibull NHPP.
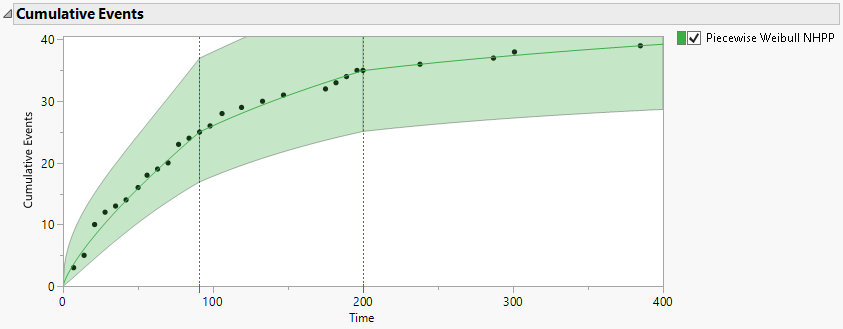
The Cumulative Events plot from the Observed Data report is shown in Figure 11.23. The vertical dashed blue lines indicate the phase transition points. The first occurrence of Revised in the column Design Phase is in row 14. So, the start of the Revised phase is taken to be the Interval Start value in row 14, namely, day 91. Similarly, the first occurrence of Final in the column Design Phase is in row 23. So, the start of the Final phase is taken to be the Interval Start value in row 23, namely, day 200.
Figure 11.23 Cumulative Events Plot
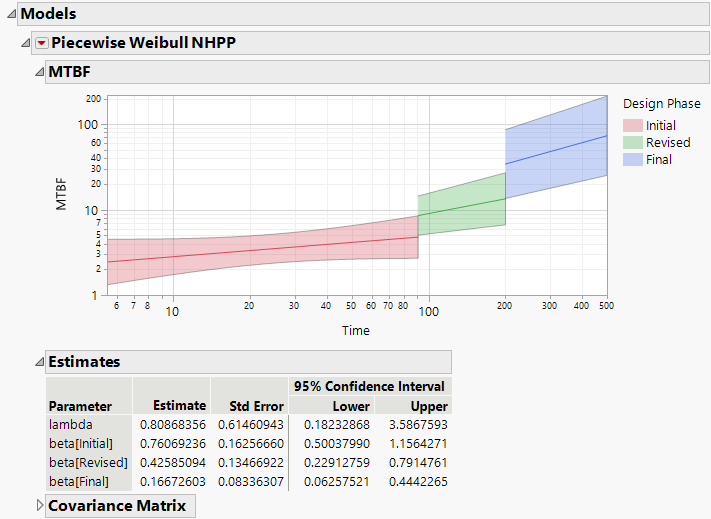
The Piecewise Weibull NHPP report is found under the Models outline node. Here you can see the mean time between failures increasing over the three phases. From the Estimates report, you can see that the estimates of beta decrease over the three testing phases.
Figure 11.24 MTBF Plot