Example of Modifying Generating Rules in a Fractional Factorial Design
Use the Screening Design platform to design an experiment for five factors. The factors are:
• Feed Rate - the amount of raw material added to the reaction chamber in liters per minute
• Catalyst (as a percent)
• Stir Rate - the RPMs of a propeller in the chamber
• Temperature (in degrees Celsius)
• Concentration of reactant
Production constraints limit the size of the experiment to no more than twelve runs. You decide to consider the 8-run fractional factorial design and the 12-run Plackett-Burman design. Also, you suspect the following statements to be true:
• The Temperature*Concentration interaction is active, so you want a design that does not alias this interaction with a main effect.
• The Catalyst*Temperature* interaction is not likely to be active.
• The Stir Rate*Concentration interaction is not likely to be active.
Use this information in constructing your design.
Create the Standard Fractional Factorial Design
To create the standard fractional factorial design, do the following:
• Specify the Factors or Specify Factors Manually
Specify the Response
1. Select DOE > Classical > Factor Screening > Screening Design.
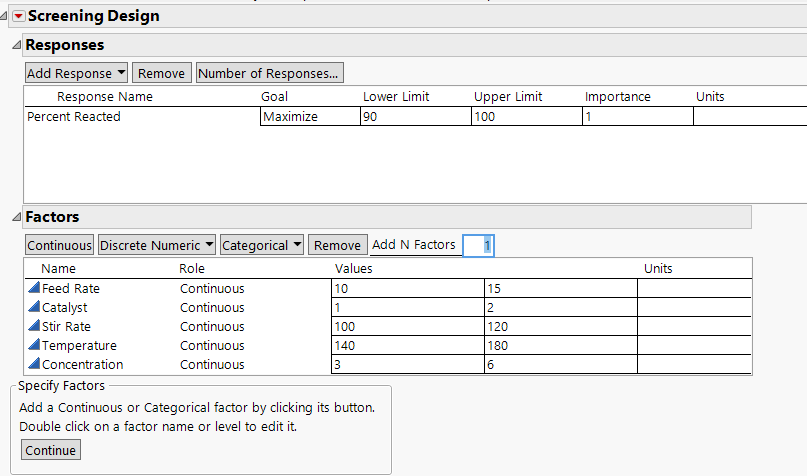
2. Double-click Y under Response Name and type Percent Reacted.
Note that the default Goal is Maximize. The Goal is to maximize the response, but the minimum acceptable reaction percentage is 90 (Lower Limit) and the upper limit is 100 (Upper Limit).
3. Click under Lower Limit and type 90.
4. Click under Upper Limit and type 100.
5. Leave the area under Importance blank.
Because there is only one response, that response is given Importance 1 by default.
See Figure 10.14 for the completed Responses section. Now, specify the factors.
Specify the Factors
You can enter the factors manually or automatically:
• To enter the factors automatically, use the Reactor Factors.jmp data table:
1. Select Help > Sample Data Folder and open Design Experiment/Reactor Factors.jmp.
2. Click the Screening Design red triangle and select Load Factors. Proceed to Choose a Design.
• To enter the factors manually, follow the steps below.
Specify Factors Manually
1. Add five continuous factors by entering 5 in the Add N Factors box and clicking Continuous.
2. Change the default factor names (X1-X5) to Feed Rate, Catalyst, Stir Rate, Temperature, and Concentration.
3. Enter the low and high values for each factor:
– Feed Rate: 10, 15
– Catalyst: 1, 2
– Stir Rate: 100, 120
– Temperature: 140, 180
– Concentration: 3, 6
Figure 10.14 Responses and Factors
Choose a Design
1. Click Continue.
2. From the Choose Screening Type panel, accept the default selection to Choose from a list of fractional factorial designs and click Continue.
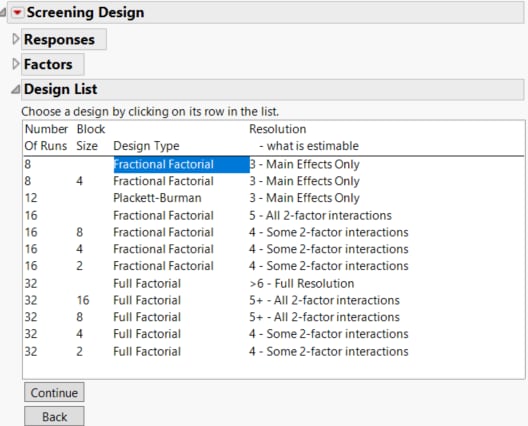
Designs for the factors and levels that you specified are listed in the Design List (Figure 10.15).
Figure 10.15 Fractional Factorial Designs for Five Continuous Factors
3. The design that you want is the first in the list and happens to be selected by default (Figure 10.15). Accept that selection and click Continue.
Because you are limited to eight runs and have no blocking factor, your best design option is the 8-run fractional factorial design with no blocks. This design is a 25-2 fractional factorial design. It is one quarter of the full factorial design for five factors.
Change the Generating Rules to Obtain a Different Fraction
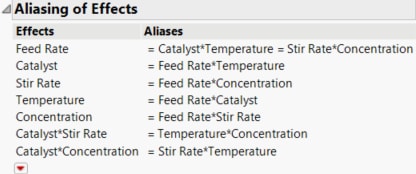
In this example, you want to know whether the Temperature*Concentration interaction is confounded with a main effect. Use the Display and Modify Design section to view the aliasing structure for the design that you selected and to change it, if appropriate.
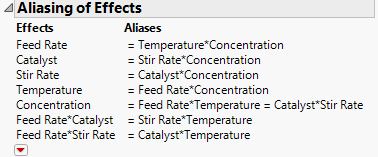
1. Open the Aliasing of Effects section.
Figure 10.16 Aliasing of Effects
The Temperature*Concentration interaction, which you suspect is active, is confounded with Feed Rate, a main effect. You want to change the generating rules to construct a design where Feed Rate is aliased with effects that you suspect are inactive, and where the Temperature*Concentration interaction is not aliased with a main effect.
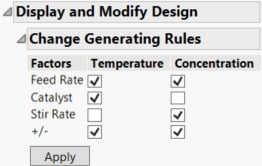
2. Open the Change Generating Rules section.
The default-generating rules give you the standard (or principal) one-quarter fraction of the full factorial design. Recall that you suspect that the Catalyst*Temperature and Stir Rate*Concentration interactions are not likely to be active. Redefine the generating rules so that these two interactions are confounded with Feed Rate. The redefined generating rules give you a different one-quarter fraction of the full factorial design.
3. Do the following:
– Deselect Stir Rate in the Temperature column.
– Deselect Catalyst in the Concentration column.
– Select Feed Rate in the Concentration column.
Figure 10.17 New Generating Rules
4. Click Apply.
Figure 10.18 Aliasing of Effects for Modified Generating Rules
In the design that you have defined, Feed Rate is confounded with Catalyst*Temperature and Stir Rate*Concentration. Also, the Temperature*Concentration interaction is now confounded with the two-way interaction Catalyst*Stir Rate.
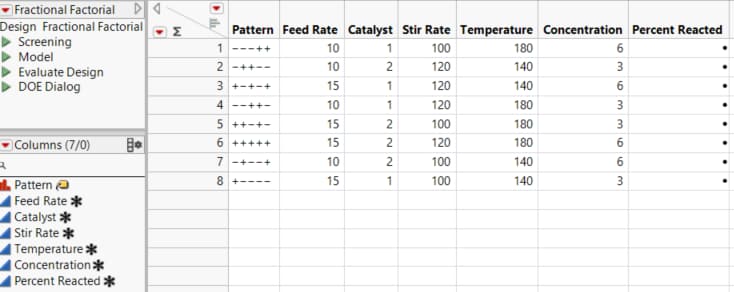
5. In the Output Options section, accept the default Run Order setting of Randomize and click Make Table.
Figure 10.19 Eight-Run Fractional Factorial Design Table
The design table shows the design that you constructed. Notice that the table contains a column for the response that you defined in the Screening window, Percent Reacted, where you can record your experimental results.
The Screening, Model, and DOE Dialog scripts are also included. For more information about these scripts, see Make Table.
Analyze the Results
Next you conduct the experiment, record your data, and proceed to analyze the results.
1. Select Help > Sample Data Folder and open Design Experiment/Reactor 8 Runs.jmp.
You can estimate seven effects with your eight runs. Of these, you expect only a few to be active. Because you want to estimate seven effects, there are no degrees of freedom for error. For these reasons, you use the Screening platform to analyze the results.
2. Run the Screening script in the data table.
The Screening script launches the Screening platform (DOE > Classical > Factor Screening > Fit Two Level Screening) for your response and factors.
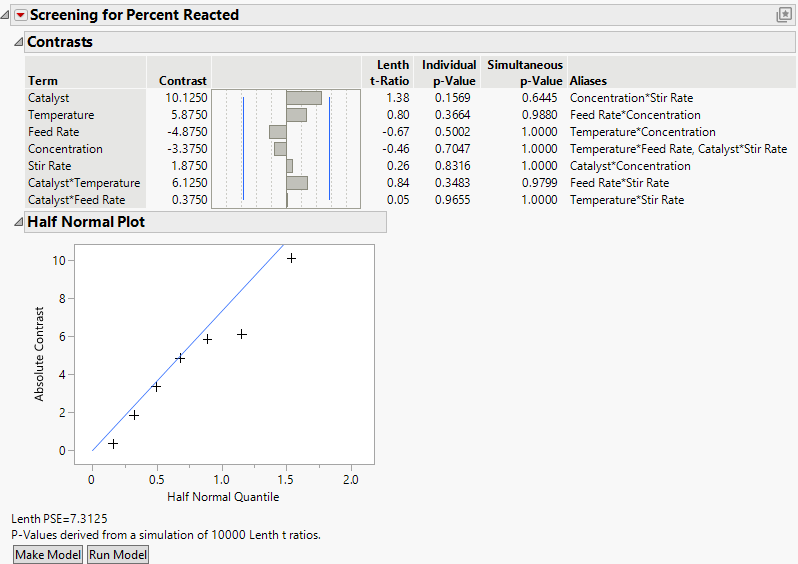
Figure 10.20 Report for Screening Example
Note: Since the p-values are obtained using a simulation-based technique, your p-values might not precisely match those shown here.
The report shows both Individual and Simultaneous p-values based on Lenth t-ratios. None of the effects are significant, even with respect to the Individual p-values. The Half Normal Plot suggests that the effects reflect only random noise.
For more information about the Screening report, see “The Fit Two Level Screening Report”.