 Statistical Details for Direct Model Fits
Statistical Details for Direct Model Fits
The direct model fits in the Functional Data Explorer platform rely on matrix decompositions. The data are converted into a stacked matrix. Each row of the matrix corresponds to the full output function for one level of the ID variable and each column of the matrix corresponds to a level of the input variable. Direct models obtain function principal component analysis (FPCA) results by performing some type of matrix decomposition routine on the stacked matrix of functions. One of the matrix decompositions used in several of the direct methods is singular value decomposition (SVD).
The SVD for an n by p matrix X can be written as follows:
X ≈ UDV′
The matrices U, D, and V have the following properties:
• U is an n by r orthogonal matrix of scores, with U′U = Ir.
• V is a p by r orthogonal matrix of loadings, with V′V = Ir.
• D is an r by r diagonal matrix of positive singular values, denoted as sk.
• r << min(n, p)
The columns of V correspond to the shape functions and the singular values correspond to the eigenvalues. Each function in the data can be approximated using a linear combination of the shape functions (the columns of V).
 Penalized SVD
Penalized SVD
The Penalized SVD method decomposes the matrix of stacked functions one dimension at a time. In the singular value decomposition (SVD) method, this means finding the best rank-one approximation of X. Approximating the rank-one approximation of X is equivalent to minimizing the squared Frobenius norm, which is written as follows:
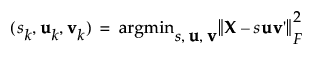
After incorporating the penalty parameters, the minimization function is written as follows:
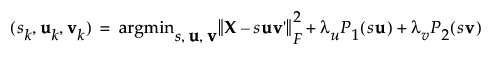
where P1(su) and P2(sv) are penalty parameters that induce sparsity.
For each dimension, k, the following routine is performed:
1. Perform a standard SVD to obtain starting values.
2. Fix u and perform a penalized regression with a lasso penalty to solve for v, using AICc for validation.
3. Fix v and a perform a penalized regression with a lasso penalty to solve for u, using AICc for validation.
4. Repeat step 2 and step 3 until u and v converge.
For more information, see Lee et al (2010).
 Nonnegative SVD
Nonnegative SVD
The Nonnegative SVD method performs a singular value decomposition (SVD) on the stacked matrix of functions, with the following additional constraints:
X ≈ UDV′ where Uij ≥ 0 and Vij ≥ 0
This method solves for U and V using constrained least squares.
 Multivariate Curve Resolution
Multivariate Curve Resolution
The Multivariate Curve Resolution (MCR) method also uses a matrix decomposition, but decomposes the stacked matrix of functions into two matrices instead of three. The matrix decomposition for an n by p matrix X can be written as follows:
X ≈ CS′
The matrices C and S have the following properties:
Cij ≥ 0
Sij ≥ 0
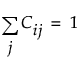 , so that each row of C sums to 1
, so that each row of C sums to 1
The columns of S are nonnegative shape functions and the rows of C are mixing proportions. This creates an approximation of X where for each individual function, the scores sum to 1 and the function is a mixture of shape functions.