Additional Example of the Fit Proportional Hazards Platform
This example uses a proportional hazards model for data that have multiple effects and multiple levels. The data were collected from a randomized clinical trial. In the trial, males with inoperable lung cancer were placed on either a standard or a novel (test) chemotherapy treatment. The primary interest of this trial was to assess if the treatment type has an effect on survival time; special interest is given to the type of tumor (Cell Type).
For the proportional hazards model, covariates include the following:
• Whether the patient had undergone previous therapy (Prior)
• Age of the patient (Age)
• Time from lung cancer diagnosis to beginning the study (Diag Time)
• A general medical status measure (KPS)
Age, Diag Time, and KPS are continuous measures and Cell Type, Treatment, and Prior are categorical (nominal) variables. The four nominal levels of Cell Type include Adeno, Large, Small, and Squamous.
This example illustrates the results for a model with more than one effect and a nominal effect with more than two levels. Hazard ratios are also demonstrated, with example calculations for hazard ratios for a continuous effect and hazard ratios for an effect that has more than two levels.
1. Select Help > Sample Data Folder and open VA Lung Cancer.jmp.
2. Select Analyze > Reliability and Survival > Fit Proportional Hazards.
3. Select Time as Time to Event.
4. Select censor as Censor.
5. Select Cell Type, Treatment, Prior, Age, Diag Time, and KPS and click Add.
6. Click Run.
7. (Optional) Click the disclosure icon on the Baseline Survival at mean title bar to close the plot, and click the disclosure icon on Effect Summary to close the report.
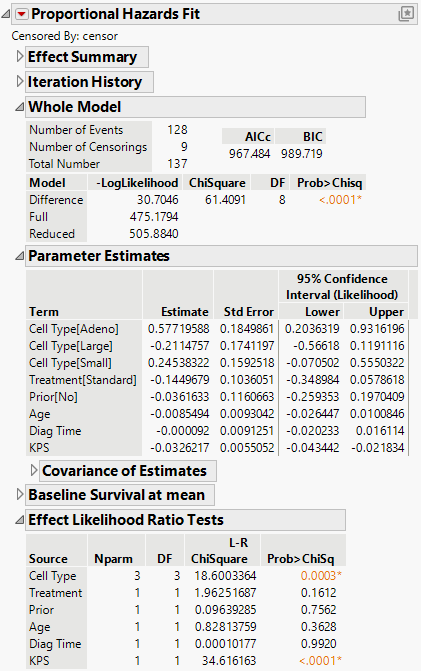
Figure 17.5 Report Window for Proportional Hazards Model with Multiple Effects and Levels
Note the following about the results:
• In the Whole Model report, the low Prob>Chisq value (<.0001) indicates that there is a difference in survival time when at least one of the effects is included in the model.
• In the Effect Likelihood Ratio Tests report, the Prob>ChiSq values indicate that KPS and at least one of the levels of Cell Type are significant; however, the Treatment, Prior, Age, and Diag Time effects are not significant.
8. Click the Proportional Hazards Fit red triangle and select Hazard Ratios.
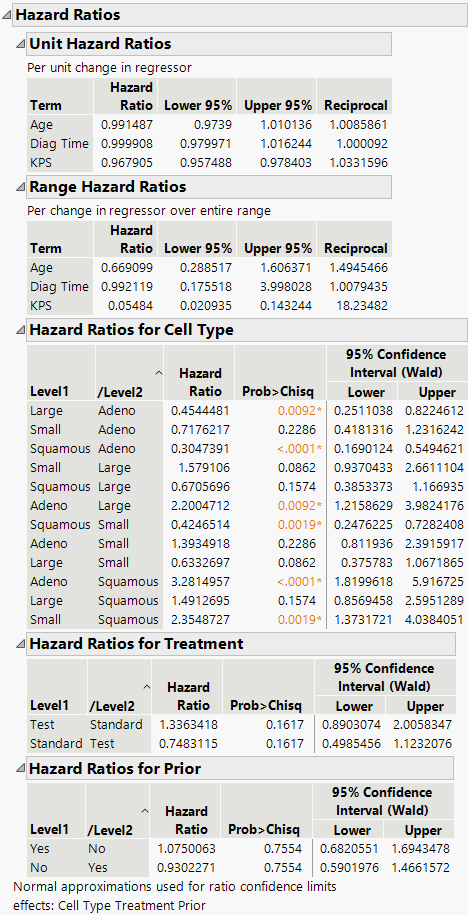
Figure 17.6 Hazard Ratios Report
Hazard Ratios for Multiple Effects and Multiple Levels
Figure 17.6 shows the Hazard Ratios for the continuous effects (Age, Diag Time, KPS) and the nominal effects (Cell Type, Treatment, Prior). For illustration, focus on the continuous effect, Age, and the nominal effect with four levels (Cell Type) for the VA Lung Cancer.jmp sample data.
For the continuous effect, Age, in the VA Lung Cancer.jmp sample data, the unit hazard ratio is calculated as follows:
exp(β) = exp(-0.0085494) = 0.991487
For the continuous effect, Age, in the VA Lung Cancer.jmp sample data, the range hazard ratio is calculated as follows:
exp[β(xmax - xmin)] = exp(-0.0085494 * 47) = 0.669099
For the nominal effect, Cell Type, all pairs of levels are calculated and are shown in the Hazard Ratios for Cell Type table. Note that for a categorical variable with k levels, only k -1 design variables, or levels, are used. In the Parameter Estimates table, parameter estimates are shown for only three of the four levels for Cell Type (Adeno, Large, and Small). The Squamous level is not shown, but it is calculated as the negative sum of the other estimates. Here are two example Hazard Ratios for Cell Type calculations:
Large/Adeno = exp(βLarge)/exp(βAdeno) = exp(-0.2114757)/exp(0.57719588) = 0.4544481
Squamous/Adeno = exp[-(βAdeno + βLarge + βSmall)]/exp(βAdeno)
= exp[-(0.57719588 + (-0.2114757) + 0.24538322)]/exp(0.57719588) = 0.3047391
Reciprocal shows the value for 1/Hazard Ratio.