Computations for the LSN
The least significant number (LSN) solves for N in the equation:
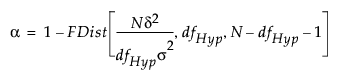
where
FDist is the cumulative distribution function of the central F distribution
dfHyp represents the degrees of freedom for the hypothesis
σ2 is the error variance
δ2 is the squared effect size
For retrospective analyses, δ2 is estimated by the sum of squares for the hypothesis divided by n, the size of the current sample. If the test is for an effect, then δ2is estimated by the sum of squares for that effect divided by the number of observations in the current study. For retrospective studies, the error variance σ2 is estimated by the mean square error. These estimates, along with an α value of 0.05, are entered into the Power Details window as default values.
When you are conducting a prospective analysis to plan a future study, you should consider determining the sample size that will achieve a specified power. See Computations for the Power.