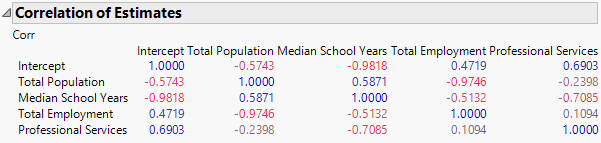
Correlation of Estimates
In the Fit Least Squares report, the Correlation of Estimates option computes the correlation matrix for the parameter estimates. These correlations indicate whether collinearity is present.
For insight on the construction of this matrix, consider the typical least squares regression formulation. Here, the response (Y) is a linear function of predictors (x’s) plus error (ε):
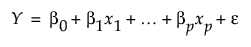
Each row of the data table contains a response value and values for the p predictors. For each observation, the predictor values are considered fixed. However, the response value is considered to be a realization of a random variable.
Considering the values of the predictors fixed, for any set of Y values, the coefficients, β0, β1, …, βp, can be estimated. In general, different sets of Y values lead to different estimates of the coefficients. The Correlation of Estimates option calculates the theoretical correlation of these parameter estimates. For technical details, see Statistical Details for the Custom Test Example.
The correlations of the parameter estimates depend solely on the predictor values and a term representing the intercept. The correlation between two parameter estimates is not affected by the values of the response.
A high positive correlation between two estimates suggests that a collinear relationship might exist between the two corresponding predictors. Note, though, that you need to interpret these correlations with caution (Belsley et al. 1980, p. 185, 92–94). Also, a rescaling of a predictor that shifts its mean changes the correlation of its parameter estimate with the intercept’s value.
Figure 3.25 Correlation of Estimates Report
The Correlation of Estimates report in Figure 3.25 shows high negative correlations between the parameter estimates for the Intercept and Median School Years (–0.9818). High negative correlations also exist between Total Population and Total Employment (–0.9746).