Differencing and Decomposition
The Time Series red triangle menu contains the following options to prepare the data for modeling.
Difference
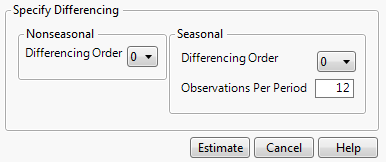
Shows the Differencing Specification window (Figure 18.5). The window enables you to specify the differencing operation that you want to apply to the time series. Differencing the values in a time series can transform a nonstationary series into a stationary series. The differenced series is given by the following equation:
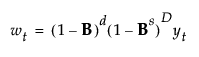
where t is the time index and B is the backshift operator defined by Byt = yt-1.
Note: Many time series do not exhibit a fixed mean, such as time series with trend or seasonality. Such nonstationary series are not suitable for description by time series models that assume a stationary time series such as ARMA models. Removing the trend and/or seasonality creates a differenced series that is stationary and enables you to describe the series using the models that assume stationarity.
Figure 18.5 Differencing Specification Window
The Differencing Specification window enables you to specify the Nonseasonal Differencing Order, d, the Seasonal Differencing Order, D, and the number of Observations per Period, s. Selecting zero for the value of the differencing order is equivalent to no differencing of that kind. Each time you specify a differencing operation and click Estimate, a new Difference Report is displayed in the report window. See Additional Examples of the Time Series Platform.
Decomposition
(Not available when either Forecast on Holdback or Use Box-Cox Transformation are selected in the launch window.) Shows a submenu of decomposition methods. Decomposition of time series data isolates and removes linear trends and seasonal cycles from a time series. This can help with better model estimation. Three Decomposition options are provided.
Remove Linear Trend
Estimates the linear trend of the time series using a linear regression model and removes the linear trend from the data. A Time Series report for the detrended series is added to the report window, along with the linear trend information. See The Time Series Report and Linear Trend Report.
Remove Cycle
Estimates the cyclic component of a time series using a single cosine wave and then removes the cyclic component from the data. When you select the Remove Cycle option, the Define Cycle dialog appears. This dialog window enables you to specify the number of units per cycle and indicate whether a constant should be subtracted from the data. A Time Series report for the decycled series is added to the report window, along with the cycle information. See The Time Series Report and Cycle Report.
X11
Removes trend and seasonal effects using the X-11 method developed by the US Bureau of the Census (Shiskin et. al. 1967). For more information about the X-11 method, see Statistical Details for X-11 Decomposition. When selected, the Select Decomposition Type dialog appears. This dialog window enables you to specify a multiplicative or additive X-11 adjustment. Once you click OK, an X11 report is added to the report window. See X11 Report.
The X11 option is available only for monthly or quarterly data. The X, Time ID column must contain numeric values equally spaced by month or quarter without any gaps or missing values. JMP returns an error if you request X11 for a time column that does not satisfy these requirements. For an example of an appropriate time column for an X11 analysis, see Create Appropriate Time ID Column.
Note: When you select the Remove Linear Trend or the Remove Cycle options, JMP adds a column to the data table that contains the detrended or decycled data. If this column is already present in the data table when you select the option, JMP overwrites the existing column.
Tip: Typically, you would begin decomposition by removing any linear trend, and then removing long cycles, such as a 12-month cycle. Then you could start removing short cycles, such as 6-month cycles.
Show Lag Plot
Shows or hides a plot with observations at time t on the Y axis and observations at time t +/- p on the X axis. The +/- p is known as the lag. This plot is useful in determining how an observation at time t is related to another observation at time t +/- p. If there is not an identifiable structure to the plot, the observations are not related. However, if there is a structure to the plot, this indicates that there is some relationship between observations across time. Identifying the structure helps when building a time series model.
Show Box-Cox Transformation Plot
(Not available if you specified Use Box-Cox Transformation in the launch window.) Shows or hides the Box-Cox Transformation plot. The Box-Cox transformation is a power transformation based on the Lambda parameter (λ) and uses the following formula:
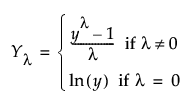
The Box-Cox Transformation Plot shows a graph of the transformed time series and options for setting the Lambda parameter (λ). The Lambda box shows the current value of the parameter. You can also use the Lambda slider to change the value of the parameter, which then automatically updates the plot. The Low and High boxes set the range of the slider.
Tip: Use the Box-Cox Transformation plot to see the transformed time series for different values of Lambda. Once you decide on a value, relaunch the analysis and select Use Box-Cox Transformation and enter the desired Lambda next to Lambda for Box-Cox. This runs the Time Series platform on the transformed series.
Cross Correlation
(Available only in the Transfer Function Analysis red triangle menu.) Shows or hides a cross-correlation plot to the report. The length of the plot is twice that of an autocorrelation plot, or 2 × ACF length + 1. The plot includes plots of the output series versus all input series, in both numerical and graphical forms. The blue lines indicate two standard errors.
Note: For the cross correlation plot, the standard errors are calculated under the null hypothesis as 1/sqrt(n - k), where n is the number of nonmissing data values and k is the number of autocorrelation lags.
Prewhitening
(Available only in the Input Series red triangle menu.) Shows the Prewhitening Specification window that enables you to set the prewhitening order. Prewhitening is a technique used to help identify the transfer function model. This technique involves fitting an ARIMA model to the input series such that the residuals are equivalent to white noise. The same model is then used to estimate the output series. You can use the cross correlation between the filtered input and filtered output series to determine an appropriate lag for the transfer function model. For information about prewhitening, see Box et al. (1994).