Example of a Probit Model with Binomial Errors
Use numerical derivatives in the Nonlinear platform to obtain maximum likelihood estimates for a probit model with binomial errors. The data table in this example includes the numbers of ingots tested for readiness after different treatments of heating and soaking times. The average number of ingots ready is the product of the number tested and the probability that an ingot is ready for use given the amount of time it was heated and soaked.
1. Select Help > Sample Data Folder and open Ingots2.jmp.
2. Select Analyze > Specialized Modeling > Nonlinear.
3. Assign P to the X, Predictor Formula role.
Using a probit model, the P column contains the following model formula:
Normal Distribution(b0+b1*Heat+b2*Soak)
The argument to the Normal Distribution function is a linear model of the treatments.
4. Assign Loss to the Loss role.
To specify binomial errors, the Loss column contains a loss function with the following formula:
-(Nready*Log(p) + (Ntotal - Nready)*Log(1 - p))
5. Select the Numeric Derivatives Only option.
6. Click OK.
7. Click Go.
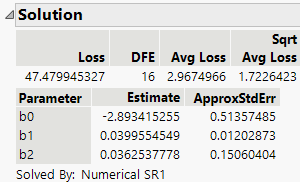
The platform used the Numerical SR1 method to obtain the parameter estimates shown in Figure 15.17.
Figure 15.17 Solution for the Ingots2 Data