Example of Process Capability for an Unstable Process
This example shows a case where the overall variation differs from the within variation because the process is not stable.
1. Select Help > Sample Data Folder and open Quality Control/Coating.jmp.
2. Select Analyze > Quality and Process > Process Capability.
3. Select Weight and click Y, Process.
4. Open the Process Subgrouping outline.
5. Select Sample in the Select Columns list on the left.
6. Select Weight in the Y, Process list on the right.
7. Click Nest Subgroup ID Column.
8. Click OK.
9. Enter 16 for LSL, 20 for Target, and 24 for USL in the Spec Limits window.
10. Click OK.
11. Click the Goal Plot red triangle and select Show Within Sigma Points.
12. Click the Process Capability red triangle and select Individual Detail Reports.
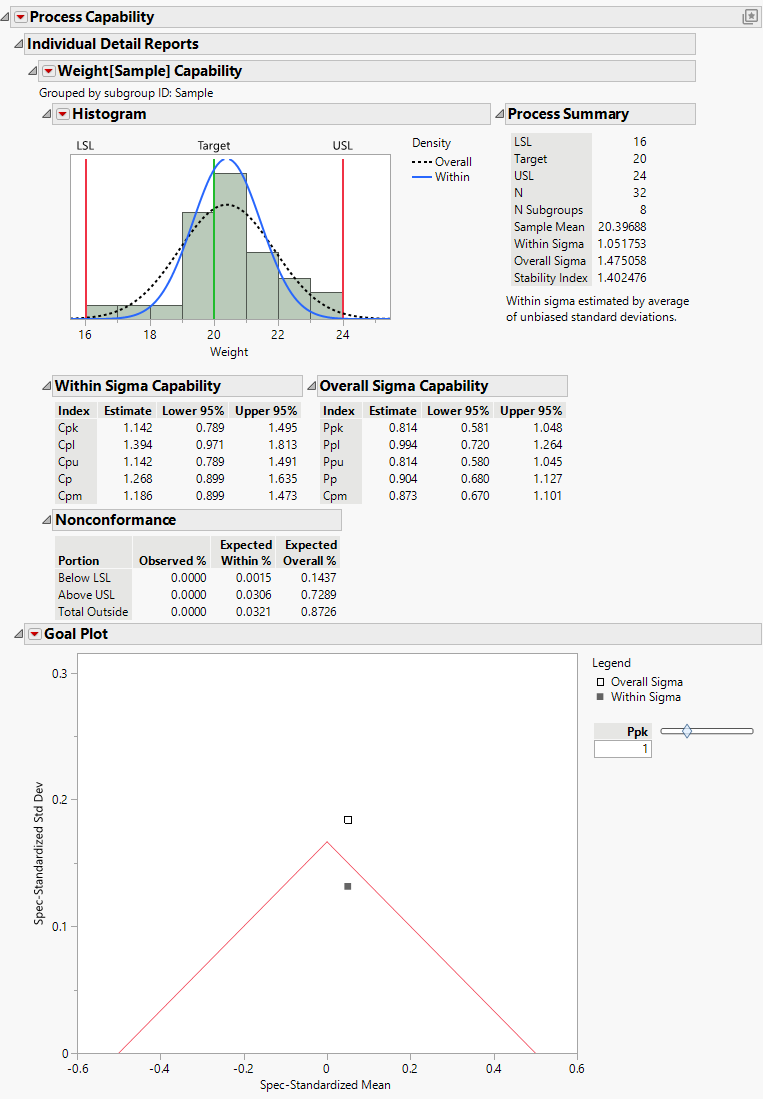
Figure 9.25 Process Capability Report for Coating.jmp Data
Figure 9.25 shows the resulting Process Capability report. The Goal Plot shows two points that represent the mean shift and standard deviation standardized to the specification limits. There is a legend next to the Goal Plot that identifies the two points. The Overall Sigma point is calculated using the overall sample standard deviation. The Within Sigma point is calculated using a within-subgroup estimate of the standard deviation.
The point calculated using Overall Sigma is outside the goal triangle corresponding to a Ppk of 1. This indicates that the variable Weight results in non-conforming product.
However, the point calculated using Within Sigma is inside the goal triangle. This indicates that, if the process were stable, Weight values would have a high probability of falling within the specification limits.
13. Hover cursor over one of the points in the Goal Plot.
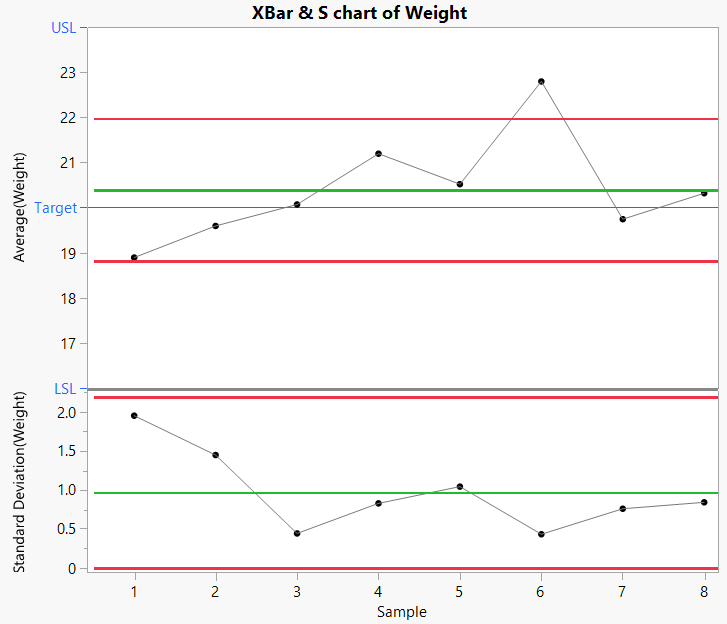
14. Click the control chart.
Figure 9.26 XBar and S Chart for Weight
The control chart indicates that the Weight measurements are unstable. The process is affected by special causes and is unpredictable. This makes the interpretation of capability indices and nonconformance estimates highly questionable. Even estimates based on Overall Sigma are questionable, because the process is not predictable.
The histogram in Figure 9.25 shows the distribution of the Weight values with normal density curves using both sigma estimates superimposed over the histogram. The normal curve that uses the Overall Sigma estimate is flatter and wider than the normal curve that uses the Within Sigma estimate. This normal curve is more dispersed because the estimate of Overall Sigma is inflated by the special causes that make the process unstable. If the process were stable, the narrower normal curve would reflect process behavior.
You can also compare the Cpk estimate (1.142) to the Ppk estimate (0.814). The fact that Ppk is much smaller than Cpk is additional evidence that this is an unpredictable process. The Cpk estimate is a forecast of the capability that you would achieve by bringing the process to a stable state.
Note: The Individual Detail Reports Cutoff preference determines whether the Individual Reports appear by default. If the preference is enabled, the Individual Reports appear by default if the number of process variables is less than or equal to the number specified in the preference. You can change this preference in Preferences > Platforms > Process Capability.