Launch the Hierarchical Cluster Platform

Launch the Hierarchical Cluster platform by selecting Analyze > Clustering > Hierarchical Cluster.

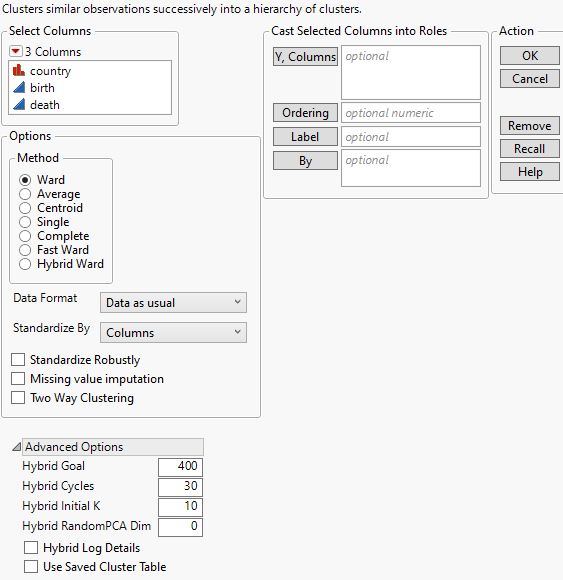
Figure 13.4 Hierarchical Cluster Launch Window 

For more information about the options in the Select Columns red triangle menu, see Column Filter Menu in Using JMP.

Y, Columns

The variables used for clustering observations.

Ordering

Sorts clusters by their mean values based on the specified column.

Tip: Use the first principal component obtained by conducting a principal components analysis as an Ordering column. The clusters are sorted by these values.

Attribute ID

(Available only if Data is stacked is selected as the data structure.) Specifies the variables that are stacked.

Object ID

(Available only if Data are summarized or Data is stacked is selected as the data structure.) A column or columns that provide a unique identifier for each unit for which measurements are stacked.

Label

A column of values used to label the dendrogram in the report.

Note: If the selected data structure is Data is distance matrix, the Label column must have a character data type.

By

A column whose levels define separate analyses. For each level of the specified column, the corresponding rows are analyzed. The results are presented in separate reports. If more than one By variable is assigned, a separate analysis is produced for each possible combination of the levels of the By variables.

Method

Specifies the method used to calculate distances for defining clusters. For each method, the clusters are joined so that the distance defined by the method is minimized. For distance formulas, see Statistical Details for Distance Methods.

Ward

Defines the distance between two clusters as the ANOVA sum of squares between the two clusters summed over all the variables. At each generation, the within-cluster sum of squares is minimized over all partitions obtainable by merging two clusters from the previous generation. The sums of squares are easier to interpret when they are divided by the total sum of squares to give the proportions of variance (squared semipartial correlations).

Ward’s method joins clusters to maximize the likelihood at each level of the hierarchy under the assumptions of multivariate normal mixtures, spherical covariance matrices, and equal sampling probabilities.

Ward’s method tends to join clusters with a small number of observations and is strongly biased toward producing clusters with approximately the same number of observations. It is also very sensitive to outliers. See Milligan (1980).

Average

Defines the distance between two clusters as the average distance between pairs of observations. Average linkage tends to join clusters with small variances and is slightly biased toward producing clusters with the same variance. See Sokal and Michener (1958).

Centroid

Defines the distance between two clusters as the squared Euclidean distance between their means. The centroid method is more robust to outliers than most other hierarchical methods but in other respects might not perform as well as Ward’s method or average linkage. See Milligan (1980).

Single

Defines the distance between two clusters as the minimum distance between an observation in one cluster and an observation in the other cluster. Single linkage has many desirable theoretical properties but has performed poorly in Monte Carlo studies. See Jardine and Sibson (1971), Fisher and Van Ness (1971), Hartigan (1981), and Milligan (1980). Single linkage was originated by Florek et al. (1951a, 1951b) and later reinvented by McQuitty (1957) and Sneath (1957).

By imposing no constraints on the shape of clusters, single linkage sacrifices performance in the recovery of compact clusters in return for the ability to detect elongated and irregular clusters. Single linkage tends to chop off the tails of distributions before separating the main clusters. See Hartigan (1981).

Complete

Defines the distance between two clusters as the maximum distance between an observation in one cluster and an observation in the other cluster. Complete linkage is strongly biased toward producing clusters with approximately equal diameters and can be severely distorted by moderate outliers. See Milligan (1980).

Fast Ward

Defines the distance between two clusters using Ward’s method. Fast Ward uses a near-neighbor chains algorithm to compute Ward's distances. This algorithm shortens computation time because it does not require the calculation of a distance matrix. Fast Ward is automatically used whenever there are more than 2,000 rows.

Hybrid Ward

Applies an algorithm that divides the clustering into two phases. The first phase is a pre-processing step that creates preliminary clusters using near-neighbor joining cycles. See Statistical Details for Near-Neighbor Joining Cycles. This is done to reduce the size of the table that is passed to the hierarchical clustering routine. After a certain number of cycles are performed or a certain number of clusters are created, the remaining clusters are formed using Ward’s method. This method is useful when you have tens or hundreds of thousands of items to cluster.

Note: Unlike the Fast Ward method, this method does not produce the same hierarchy as a full Ward’s method. However, it takes less computation time for a large number of items, especially if you have multiple computing cores and can use multithreading for the near-neighbor search.

Data Format

Specifies the form of the data that is used in calculating multivariate distances.

Data as usual

Data that are rectangular with one row for each observation and one column for each variable.

Data as summarized

Data that are summarized by the levels of one or more identifying columns. When you select this option, an Object ID text box appears in the launch window. Specify the identifying columns as the Object ID. The Data as summarized option calculates level means and treats these means as your input data.

Data is distance matrix

Data that consist of distances between observations. For n observations, the distance table should have n rows and n + 1 columns. One column (usually the first) must contain a unique identifier for each of the n observations. The remaining columns contain distances between that observation and the n observations. Note the following:

• The diagonal elements of the table should be zero or missing, because the distance between a point and itself is zero. Values that are not zero or missing are treated as zero, and a note appears in the report.

• The distance columns can be a symmetric square matrix, or they can be upper or lower triangular with missing entries in the lower or upper portion. If the distances are given as a square matrix, a warning appears in the report if the table is not symmetric.

• You can begin with a different data structure and then save a distance matrix. See Save Distance Matrix.

When you select the Data is distance matrix option, enter the distance columns as Y, Columns and the identifier column as Label. The Label column must have the Character data type. For an example, see Example of a Distance Matrix.

Data is stacked

Data that have a single response of interest and multiple rows for each object.

When you select the Data is stacked option, Attribute ID and Object ID text boxes appear in the launch window.

• Enter a single column as Y, Columns.

• Enter columns that describe groupings of the Y, Columns variable as Attribute ID. If only two columns are entered and if you select Add Spatial Measures, then you can add spatial components to be used in the cluster analysis. See Add Spatial Measures.

• Enter the identifying columns for objects as Object ID.

The analysis that is conducted is equivalent to splitting the Y, Column variable by the Attribute ID columns and then performing hierarchical clustering without standardizing the response columns.

Tip: Use this option together with the Add Spatial Measures option to perform two-dimensional spatial clustering. For example, wafer data are often recorded using one row for each die. Interest centers around clustering wafers. See Example of Wafer Defect Classification Using Spatial Measures.

Caution: Because there is a single measurement column, standardizing the data is not appropriate for stacked data.

Standardize By

Specifies how to standardize the values prior to clustering. This is useful to address the issue of different measurement scales for continuous and ordinal columns.

Unstandardized

Uses the original data.

Columns

Standardizes the values in each column by subtracting the column mean and dividing by the column standard deviation.

Rows

Standardizes the values in each row by subtracting the row mean and dividing by the row standard deviation.

Columns and Rows

Standardizes the values by first subtracting both the column mean and row mean and then adding back the grand mean. Then, the values are scaled by the standard deviation of the doubly-centered data.

Standardize Robustly

Reduces the influence of outliers on estimates of the mean and standard deviation for continuous and ordinal columns. This option uses Huber M-estimates of the mean and standard deviation (Huber 1964; Huber 1973; Huber and Ronchetti 2009). For columns with outliers, this option gives the standardized values greater representation in determining multivariate distances.

Note: If you use a Standardize By option and select Standardize Robustly, the robust mean and standard deviation are used for whichever standardizing method that you specify.

Missing value imputation

Imputes missing values. If the number of variables is either 50 or less, or less than half the number of rows, multivariate normal imputation is used. Otherwise, multivariate SVD imputation is used.

Multivariate normal imputation calculates pairwise covariances to construct a covariance matrix for the response columns. Then each missing value is imputed by a method that is equivalent to regression prediction using all the predictors with no missing values for the given observation. If the constructed covariance matrix is not positive definite, missing values are imputed using their column means.

Multivariate SVD imputation avoids constructing a covariance matrix by using the singular value decomposition. See Explore Missing Values in Predictive and Specialized Modeling.

Caution: Missing value imputation assumes that there are no clusters, that the data come from a single multivariate normal distribution, and that the values are missing completely at random. Because these assumptions are usually not reasonable in practice, use this feature with caution. However, the feature can produce more informative results than discarding most of your data.

Add Spatial Measures

(Available only if the Data is stacked option is selected as the Data Format.) Select this option when your data are stacked and contain two attribute columns that correspond to spatial coordinates (horizontal and vertical coordinates, for example). This option opens a window in which you can select and weight spatial components to aid in clustering defect patterns. This is a specialty method and is applicable in only very specific settings. See Statistical Details for Spatial Measures and Example of Wafer Defect Classification Using Spatial Measures.

Two Way Clustering

(Available only if the Data as usual or Data as summarized options are selected as the Data Format.) Clusters by both the specified columns and the rows. A color map is added to the dendrogram with a dendrogram for the Y variables at its base. Typically, for two-way clustering, your variables are measured on the same scale and you do not standardize the data.

Advanced Options

Specifies advanced options for the Hybrid Ward method.

Hybrid Goal

Specifies the maximum number of clusters allowed before switching to the hierarchical clustering routine. When the hierarchical clustering routine starts, the number of clusters must be less than or equal to the Hybrid Goal. The default value for Hybrid Goal is 400.

Hybrid Cycles

Specifies the minimum number of near-neighbor joining cycles that are performed before switching to the hierarchical clustering routine. The default value for Hybrid Cycles is 30.

Hybrid Initial K

Specifies the initial number of neighbors used in the near-neighbor joining cycles. The number of neighbors can increase or decrease depending on how many unique near neighbors are found in the previous cycle. The default value for Hybrid Initial K is 10.

Hybrid RandomPCA Dim

Specifies the number of dimensions to use in the Randomized PCA dimension reduction technique. This technique is used when the value of Hybrid RandomPCA Dim is any value greater than zero and provides further speed improvements. The Randomized PCA technique reduces the dimension of the problem by calculating approximate principal components, which leads to approximated distances between points. See Halko, Martinsson, and Tropp (2011).

Hybrid Log Details

Specifies whether to show the status and timings of each state of the Hybrid Ward method in the log.

Use Saved Cluster Table

Uses a separate cluster history table to specify the clustering.

Not Enough Nonmissing Data Alert

The JMP alert Not enough nonmissing data can be difficult to understand when you are using the Data as summarized or Data is stacked data formats. The alert occurs in the following situations:

• If the selected Data Format is Data as usual, the alert occurs when all rows or all but one row are missing at least one value for a Y, Columns variable.

• If the selected Data Format is Data as summarized, the alert occurs when your data are summarized across the Object ID columns, all rows or all but one row are missing at least one value of the summarized Y, Column variables. To see the data structure that the Cluster platform is analyzing, select Tables > Summary, enter the Object ID columns as Group and the Y, Columns variables as Statistics > Mean.

• If the selected Data Format is Data is stacked, the alert occurs when your data are split across the Attribute ID columns, all rows or all but one row are missing at least one value of the split Y, Column values. To see the data structure that the Cluster platform is analyzing, select Tables > Split, enter the Attribute ID columns as Split By, the Y, Columns variable as Split Columns, and the Object ID columns as Group.

Tip: A message is also printed to the log that identifies the objects that have missing values.