Matrix Functions
All(A, ...)
Returns
1 if all matrix arguments are nonzero; 0 otherwise.
Any(A, ...)
Returns
1 if one or more elements of one or more matrices are nonzero; 0 otherwise.
B Spline Coef(x, Internal Knot Grid, <degree=3>, <Knot End Points=min(x)||max(x)>)
Description
Finds the matrix of B-spline coefficients for the data in the x argument.
Returns
The matrix of B-spline basis coefficients. This matrix can be used as a design matrix in a linear model. The first column of the matrix contains an intercept term.
Arguments
x
A row or column vector that contains the data.
Internal Knot Grid
Either a single number that designates the number of desired knot points based on percentiles of x or a vector of values that designate the internal knot points. The number of internal knots must be greater than zero and less than or equal to the number of unique elements in x minus two.
degree
A number that indicates the degree of the B-splines. Defaults to 3.
Knot End Points
A 2x1 matrix that designates the lower and upper knot points. If this argument is not specified, the default lower and upper knot points are the minimum and maximum values of x, respectively.
Notes
This function is used in column formulas created by the Functional Data Explorer platform.
CDF(Y)
Description
Returns values of the empirical cumulative probability distribution function for Y, which can be a vector or a list. Cumulative probability is the proportion of data values less than or equal to the value of QuantVec.
Syntax
{QuantVec, CumProbVec} = CDF(YVec)
Chol Update(L, V, C)
Description
If L is the Cholesky root of an nxn matrix A, then after calling cholUpdate L is replaced with the Cholesky root of A+V*C*V' where C is an mxm symmetric matrix and V is an n*m matrix.
Cholesky(A)
Description
Finds the lower Cholesky root (L) of a positive semi-definitive matrix, L*L' = A.
Returns
L (the Cholesky root).
Arguments
A
a symmetric matrix.
Correlation(matrix, < <<"Pairwise">, < <<"Shrink">, < <<Freq(vector)>, < <<Weight(vector)>)
Description
Calculates the correlation matrix of the data in the matrix argument.
Returns
The correlation matrix for the specified matrix.
Argument
matrix
A matrix that contains the data. If the data has m rows and n columns, the result is an m-by-m matrix.
"Pairwise"
Uses the pairwise method for missing values rather than the row-wise method.
"Shrink"
Performs the Schafer-Strimmer shrinkage estimate.
<<Freq(vector)
A vector that specifies frequencies for the rows of the matrix argument.
<<Weight(vector)
A vector that specifies weights for the rows of the matrix argument.
Notes
By default, rows are discarded if they contain missing values. If the "Pairwise" option is specified, all pairs of nonmissing values are used in the correlation matrix calculation.
This function uses multithreading if available, so it is recommended for large problems with many rows.
When a column is constant, the correlations for it are 0, and the diagonal element is also 0.
Covariance(matrix, < <<"Pairwise">, < <<"Shrink">, < <<Freq(vector)>, < <<Weight(vector)>)
Description
Calculates the covariance matrix of the data in the matrix argument.
Returns
The covariance matrix for the specified matrix.
Argument
matrix
A matrix that contains the data. If the data has m rows and n columns, the result is an m-by-n matrix.
"Pairwise"
Uses the pairwise method for missing values rather than the row-wise method.
"Shrink"
Performs the Schafer-Strimmer shrinkage estimate.
<<Freq(vector)
A vector that specifies frequencies for the rows of the matrix argument.
<<Weight(vector)
A vector that specifies weights for the rows of the matrix argument.
Notes
By default, rows are discarded if they contain missing values. If the "Pairwise" option is specified, all pairs of nonmissing values are used in the covariance matrix calculation.
This function uses multithreading if available, so it is recommended for large problems with many rows.
Design(vector, < levelsList | <<levels, <<ElseMissing >)
Description
Creates a design matrix that contains a column of 1s and 0s for each unique value of a vector of values.
Returns
A design matrix with a column of 1s and 0s for each unique value of the argument or a list that contains the design matrix and a list of levels.
Argument
vector
A vector.
levelsList
An optional list or matrix argument that specifies the levels in the returned matrix.
<<levels
An optional argument that changes the return value to a list that contains the design matrix and a list of the levels.
<<ElseMissing
An optional argument that changes the handling of values in the vector argument that do not appear in the levelsList argument. If this argument is specified, missing values are placed in the design matrix. Otherwise, 0s are placed in the design matrix.
Notes
Missing values in the levelsList argument are not ignored. For example:
Show( Design ( ., [. 0 1] ),
Design( 0, [. 0 1] ),
Design( 1, [. 0 1] ),
Design( [0 0 1 . 1], [. 0 1] ),
Design( {0, 0, 1, ., 1}, [. 0 1] ) );
Design(., [. 0 1]) = [1 0 0];
Design(0, [. 0 1]) = [0 1 0];
Design(1, [. 0 1]) = [0 0 1];
Design([0 0 1 . 1], [. 0 1]) =
[ 0 1 0,
0 1 0,
0 0 1,
1 0 0,
0 0 1];
Design({0, 0, 1, ., 1}, [. 0 1]) =
[ 0 1 0,
0 1 0,
0 0 1,
1 0 0,
0 0 1];
Design Last(vector, < levelsList, <<ElseMissing >)
Description
Creates a design matrix that contains a column of 1s and 0s for all but the last of the unique values of the argument. The last level is coded as a row of 0s.
Returns
A full-rank design matrix or a list that contains the design matrix and a list of levels.
Arguments
vector
A vector.
levelsList
An optional list or matrix argument that specifies the levels in the returned matrix. If this argument is specified, the last level in this list or matrix is treated as the last level in the design matrix. Otherwise, the last level is defined as the largest value in the vector argument.
<<ElseMissing
An optional argument that changes the handling of values in the vector argument that do not appear in the levelsList argument. If this argument is specified, missing values are placed in the design matrix. Otherwise, 0s are placed in the design matrix.
Design Nom(vector, < levelsList | <<levels, <<ElseMissing >)
DesignF(vector, < levelsList | <<levels, <<ElseMissing >)
Description
Creates a design matrix that contains a column of 1s and 0s for all but the last of the unique values of the argument. The last level is coded as a row of -1s.
Returns
A full-rank design matrix or a list that contains the design matrix and a list of levels.
Argument
vector
A vector.
levelsList
An optional list or matrix argument that specifies the levels in the returned matrix. If this argument is specified, the last level in this list or matrix is treated as the last level in the design matrix. Otherwise, the last level is defined as the largest value in the vector argument.
<<levels
An optional argument that changes the return value to a list that contains the design matrix and a list of levels.
<<ElseMissing
An optional argument that changes the handling of values in the vector argument that do not appear in the levelsList argument. If this argument is specified, missing values are placed in the design matrix. Otherwise, 0s are placed in the design matrix.
Notes
Missing values in the levelsList argument are not ignored. For example:
Show( Design Nom( ., [. 0 1] ),
Design Nom( 0, [. 0 1] ),
Design Nom( 1, [. 0 1] ),
Design Nom( [0 0 1 . 1], [. 0 1] ),
Design Nom( {0, 0, 1, ., 1}, [. 0 1] ) );
Design Nom(., [. 0 1]) = [1 0];
Design Nom(0, [. 0 1]) = [0 1];
Design Nom(1, [. 0 1]) = [-1 -1];
Design Nom([0 0 1 . 1], [. 0 1]) = [0 1, 0 1, -1 -1, 1 0, -1 -1];
Design Nom({0, 0, 1, ., 1}, [. 0 1]) = [0 1, 0 1, -1 -1, 1 0, -1 -1];
Design Ord(vector, < levelsList | <<levels, <<ElseMissing >)
Description
Creates a design matrix that contains a column for all but the last of the unique values of the argument. The first level is coded as a row of 0s. Each subsequent (nth) level in the levelsList argument is coded as a row of (n-1) 1s and the rest 0s.
Returns
A full-rank design matrix or a list that contains the design matrix and a list of levels.
Argument
vector
A vector.
levelsList
An optional list or matrix argument that specifies the levels in the returned matrix.
<<levels
An optional argument that changes the return value to a list that contains the design matrix and a list of levels.
<<ElseMissing
An optional argument that changes the handling of values in the vector argument that do not appear in the levelsList argument. If this argument is specified, missing values are placed in the design matrix. Otherwise, 0s are placed in the design matrix.
Notes
Missing values in the levelsList argument are not ignored. For example:
Show( Design Ord( ., [. 0 1] ),
Design Ord( 0, [. 0 1] ),
Design Ord( 1, [. 0 1] ),
Design Ord( [0 0 1 . 1], [. 0 1] ),
Design Ord( {0, 0, 1, ., 1}, [. 0 1] ) );
Design Ord(., [. 0 1]) = [0 0];
Design Ord(0, [. 0 1]) = [1 0];
Design Ord(1, [. 0 1]) = [1 1];
Design Ord([0 0 1 . 1], [. 0 1]) = [1 0, 1 0, 1 1, 0 0, 1 1];
Design Ord({0, 0, 1, ., 1}, [. 0 1]) = [1 0, 1 0, 1 1, 0 0, 1 1];
Det(A)
Description
Determinant of a square matrix.
Returns
The determinant.
Argument
A
A square matrix.
Diag(A, <B>)
Description
Creates a diagonal matrix from a square matrix or a vector. If two matrices are provided, concatenates the matrices diagonally.
Returns
The matrix.
Argument
A
a matrix or a vector.
Direct Product(A, B)
Description
Direct (Kronecker) product of square matrices or scalars A[i,j]*B.
Returns
The product.
Arguments
A, B
Square matrices or scalars.
Distance(x1, x2, <scales>, <powers>)
Description
Produces a matrix of distances between rows of x1 and rows of x2.
Returns
A matrix.
Arguments
x1, x2
Two matrices.
scales
Optional argument to customize the scaling of the matrix.
powers
Optional argument to customize the powers of the matrix.
E Div(A, B)
A:/B
Returns
A matrix that contains the element-by-element division of two matrices.
Arguments
A, B
Two matrices. Both matrix elements must have the same dimensions.
E Max(A, B)
Returns
A matrix that contains the element-by-element maximum values of two or more matrices or scalar arguments.
Arguments
A, B
Two or more matrices or scalars. All matrix elements must have the same dimensions.
E Min(A, B)
Returns
A matrix that contains the element-by-element minimum values of two or more matrices or scalar arguments.
Arguments
A, B
Two or more matrices or scalars. All matrix elements must have the same dimensions.
E Mult(A, B)
A:*B
Description
Element-by-element multiplication of two matrices.
Returns
A matrix that contains the element-by-element multiplication of two or more matrices or scalar arguments.
Arguments
A, B
Two or more matrices or scalars. All matrix elements must have the same dimensions.
Eigen(A)
Description
Eigenvalue decomposition.
Returns
A list {M, E} such that E * Diag(M) * E = A'.
Argument
A
A symmetric matrix.
Estimate Bartlett Factor Score(dataRow, ManMeans, LatMeans, S, A)
Description
Estimates factor scores from a structural equation model (SEM) using Bartlett’s method.
Returns
A row vector of estimated factor scores based on the structural equation model.
Arguments
dataRow
A row vector of data values.
ManMeans
A vector of model-implied manifest variable means.
LatMeans
A vector of model-implied latent variable means.
S
The symmetric S matrix from a structural equation model.
A
The rectangular A matrix from a structural equation model.
See Also
“Model Options” in Multivariate Methods
Estimate Factor Score(dataRow, Covariance, ManMeans, LatMeans)
Description
Estimates factor scores from a structural equation model (SEM).
Returns
A row vector of estimated factor scores based on the structural equation model.
Arguments
dataRow
A row vector of data values.
Covariance
A model-implied variance-covariance matrix.
ManMeans
A vector of model-implied manifest variable means.
LatMeans
A vector of model-implied latent variable means.
Note
This function is used in the Save Factor Scores option in an Structural Equation Model report.
See Also
“Model Options” in Multivariate Methods
Fourier Basis Coef(x, Number Pairs, <Period=max(x)-min(x)+1>)
Description
Finds the matrix of Fourier basis coefficients for the data in the x argument.
Returns
The matrix of Fourier basis coefficients. This can be used as a design matrix in a linear model. The first column of the matrix contains an intercept term. The remaining columns contain pairs of basis coefficients, where pair i is defined as the sin() and cos() of i * (2 * π / Period) * x.
Arguments
x
A row or column vector that contains the data.
Number Pairs
The number of sin() and cos() pairs for the Fourier basis.
Period
The period for trigonometric functions that make up the Fourier basis.
Notes
This function is used in column formulas created by the Functional Data Explorer platform.
G Inverse(A)
Description
Generalized (Moore-Penrose) matrix inverse.
H Direct Product(A, B)
Description
Horizontal direct product of two square matrices of the same dimension or scalars.
Hough Line Transform(matrix, <NAngle(number)>, <NRadius(number)>)
Description
Takes a matrix of intensities and transforms it in a way that is useful for finding streaks in the matrix. Produces a matrix containing the Hough Line Transform with angles as columns and radiuses as rows.
Argument
matrix
A matrix that can be derived from the intensities of an image, but is more likely from a semiconductor wafer that may have defects across in a streak due to planarization machines.
NAngle(number)
Enter the number of the angle to obtain a different sized transform. The default is 180 degrees.
NRadius(number)
Enter the number of the radius to obtain a different sized transform. The default is sqrt(NRow*nRow+nCol*nCol).
Identity(n)
Description
Creates an n-by-n identity matrix with ones on the diagonal and zeros elsewhere.
Returns
The matrix.
Argument
n
An integer.
Index(i, j, <increment>)
i::j
Description
Creates a column matrix whose values range from i to j.
Returns
The matrix.
Arguments
i, j
Integers that define the range: i is the beginning of the range, j is the end.
increment
Optional argument to change the default increment, which is +1.
Inv()
See Inverse(A).
Inv Update(A, X, 1|-1)
Description
Efficiently update an X´X matrix.
Arguments
A
The matrix to be updated.
X
One or more rows to be added to or deleted from the matrix A.
1|-1
The third argument controls whether the row or rows defined in the second argument, X, are added to or deleted from the matrix A. 1 means to add the row or rows and -1 means to delete the row or rows.
Inverse(A)
Inv(A)
Description
Returns the matrix inverse. The matrix must be square non-singular.
Is Matrix(x)
Description
Returns 1 if the evaluated argument is a matrix, or 0 otherwise.
J(nrows, <ncols>, <value>)
Description
Creates a matrix of identical values.
Returns
The matrix.
Arguments
nrows
Number of rows in matrix. If ncols is not specified, nrows is also used as ncols.
ncols
Number of columns in matrix.
value
The value used to populate the matrix. If value is not specified, 1 is used.
KDTable(matrix)
Description
Returns a table created using the k-dimensional tree (k-d tree) algorithm. The table can be used to efficiently look up nearest neighbors. The k-dimensional tree is a data structure for searching points in a k-dimensional space. It works by partitioning the points into smaller subsets along each dimension and building a tree recursively. During search, the algorithm compares the query point to the partitioning values at each node and explores the relevant subtrees. It is useful for nearest neighbor search and other applications involving multi-dimensional data. For more information about how the k-d tree structure is computed, see Bentley (1975).
Returns
A KDTable object.
Argument
matrix
A matrix of k-dimensional points. The number of dimensions or points is not limited. Each column in the matrix represents a dimension to the data, and each row represents a data point.
Messages
<<Distance between rows(row1, row2)
Returns the distance between the two specified rows in the KDTable. The distance applies to removed and inserted rows as well.
<<K nearest rows(stop, <position>)
Returns a matrix. <position> is a point that is described as a row vector for the coordinate of a row, or as the number of a row. If <position> is not specified, returns the n nearest rows and distances to all rows. If <position> is specified, returns the n nearest rows and distances to either a point or a row. Stop is either n or {n, limit}. The limit parameter defines the number of rows that will be returned. It can be specified one of two ways: a number, like 5, returns the 5 nearest rows. A list, like {5,10}, returns up to 5 nearest rows, stopping when the distance of 10 is exceeded. When using a list as limit, the last row returned may have a distance greater than 10. Because the command continues until it finds the closest row beyond the stop distance, this point is also returned. This can be especially useful if there are no rows within the stop distance.
<<Remove rows(number | vector)
Remove either the row specified by number or the rows specified by vector. Returns the number of rows that were removed. Rows that were already removed are ignored.
<<Insert rows(number | vector)
Re-insert either the row specified by number or the rows specified by vector. Returns the number of rows that were inserted. Rows that were already inserted are ignored.
Notes
When rows are removed or inserted, the row indices do not change. You can remove and re-insert only rows that are in the KDTable object. If you need different rows, construct a new KDTable.
Least Squares Solve(y, X, < <<noIntercept, <<weights(OptionalWeightVector), <<method("Sweep"|"GInv")>)
Description
Computes least squares regression estimates for the assumed model y = X * beta + error.
Returns
A list that contains the matrix Beta=Inverse(X'X)X'y and the estimated variance matrix of Beta.
Optional Named Arguments
<<noIntercept
Specifies a no-intercept model.
<<weights(optional weight vector)
Specifies a vector of weights to perform weighted least squares.
<<method("Sweep" | "GInv")
Specifies the method for solving the normal equations. The default Sweep method is more computationally efficient, but you can also specify the generalized inverse ("GInv") method, which is more numerically stable.
Linear Regression(y, X, < <<noIntercept, <<printToLog, <<weight(OptionalWeightVector), <<freq(OptionalFreqVector)>)
Description
Fits a linear regression for the assumed model y = X * beta + error.
Returns
A list that contains a vector of the estimates, a vector of the standard error, and a list of diagnostics. The list of diagnostics contains vectors of the t statistics and p-values for the estimates, as well as the R-Square and adjusted R-Square values for the regression fit.
Optional Named Arguments
<<noIntercept
Excludes the intercept.
<<printToLog
Prints a summary of the fit to the log.
<<weight(vector)
Specifies a vector of weights to perform weighted least squares.
<<freq(vector)
Specifies a vector of frequencies for each row of y and X.
Example
n = 10;
x = J( n, 1, Random Normal() );
y = 1 + x * 3 + J( n, 1, Random Normal() );
{Estimates, Std_Error, Diagnostics} = Linear Regression( y, x, <<printToLog );
As Table( y || x );
Bivariate( Y( :Col1 ), X( :Col2 ), Fit Line( 1 ) );
Loc(A)
Loc(A, item)
Description
Returns a matrix of subscript positions where A is nonzero and nonmissing. For the two-argument function, Loc returns a matrix of positions where item is found within A. If the first argument is a list, the second argument is required.
For better performance and flexibility, use Where() instead. See Where(<dt>, clause) on page 221.
Argument
A
a matrix or a list
item
the item to be found within the matrix or list A
Loc Max(A)
Description
Returns the position of the maximum element in a matrix.
Returns
An integer that is the specified position.
Argument
A
a matrix
Loc Min(A)
Description
Returns the position of the minimum element in a matrix.
Returns
An integer that is the specified position.
Argument
A
a matrix
Loc NonMissing(matrix, ..., {list}, ...)
Description
Returns indices of nonmissing rows in matrices or lists. In lists, the function can also return indices of nonempty characters.
Returns
The new matrix or list.
Loc Sorted(A, B)
Description
Returns a column vector of subscript positions where the values of A have values less than or equal to the values in B based on a binary search. A must be a matrix sorted in ascending order without missing values.
Returns
The new matrix, which has the same dimensions as B. If a value in B is less than the first value in A, the returned subscript position for that value is 1.
Argument
A, B
matrices
Matrix({{x11, ..., x1m}, {x21, ..., 2m}, {...}, {xn1, ..., xnm}})
Matrix({x1, ..., xn})
Matrix(n, m)
Description
Constructs an n-by-m matrix. The following specification methods are available:
– If you specify a list of n lists that each contain m row values, the matrix is formed by vertically concatenating the evaluated lists. The list items must evaluate to numeric values or row vectors, and the dimensions of the items must be conformable.
– If you specify a single list of n items, the return value is an n-by-1 column vector. The items of the evaluated list must evaluate to numeric values.
– If you specify two integer arguments, the return value is a matrix of zeros that contains n rows and m columns.
Examples
Matrix({{1, 2, 3}, {4, [5 6]}, {7, 8, 9}});
[1 2 3, 4 5 6, 7 8 9]
Matrix({{[1 2 3], 4, 5, 6, 7, 8, 9}});
[1 2 3 4 5 6 7 8 9]
Matrix({2,3+7});
[2, 10]
Matrix(2,3);
[0 0 0, 0 0 0]
Matrix Mult(A, B)
C=A*B, ...
Description
Matrix multiplication.
Arguments
A, B, ...
Two or more matrices, which must be conformable (all matrices after the first one listed must have the same number of rows as the number of columns in the first matrix).
Notes
Matrix Mult() allows only two arguments, while using the * operator enables you to multiply several matrices.
Matrix Rank(A)
Description
Returns the rank of the matrix A.
Mode({list } or matrix)
Description
Selects the most frequent item from a numeric or character list or a numeric matrix. In the event of a tie, the lower value is selected. If multiple arguments are specified, a combination of numeric values and quoted character strings is acceptable.
Arguments
Specify either a list or a matrix.
Multivariate Normal Impute(yVec, meanYvec, symCovMat, colMin, colMax)
Description
Imputes missing values in yVec based on the mean and covariance.
Arguments
yVec
The vector of responses.
meanYvec
The vector of response means.
symCovMat
A symmetric matrix containing the response covariances. If the covariance matrix is not specified, then JMP imputes with means.
colMin
A vector of column minimums. Provides lower bounds for the imputations.
colMax
A vector of column maximums. Provides upper bounds for the imputations.
NChooseK Matrix(n, k)
Description
Returns a matrix of n things taken k at a time (n select k).
N Col(x)
N Cols(x)
Description
Returns the number of columns in either a data table or a matrix.
Argument
x
Can be a data table or a matrix.
Ortho(A, <Centered(0)>, <Scaled(1)>)
Description
Orthonormalizes the columns of matrix A using the Gram Schmidt method. Centered(0) makes the columns to sum to zero. Scaled(1) makes them unit length.
Ortho Poly(vector, order)
Description
Returns orthogonal polynomials for a vector of indices representing spacings up to the order given.
P Spline Coef(x, Internal Knot Grid, <degree=3>)
Description
Finds the matrix of penalized basis spline (P-spline) coefficients for the data in the x argument.
Returns
The matrix of P-spline basis coefficients, which is the truncated power basis of the specified degree. The truncated power basis of degree p with knots k1 through kK is defined as follows:
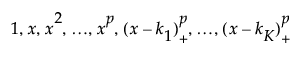
where (x - k1)+ is the positive part of (x - k1) and is set to zero for negative values of (x - k1).
Arguments
x
A row or column vector that contains the data.
Internal Knot Grid
Either a single number that designates the number of desired knot points based on percentiles of x or a vector of values that designate the internal knot points.
degree
A number that indicates the degree of the P-splines. Defaults to 3.
Notes
This function is used in column formulas created by the Functional Data Explorer platform.
Parallel Assign({thread_local_var = global_var, ...}, matrix[a, b] = expression using a and b)
Description
Uses multiple threads to assign values to the matrix. Enables you to take advantage of multiple cores on a computer. The function has two arguments.
– The first argument is a list of assignment statements that copies global variables into each thread’s local variable list.
– The second argument is an assignment expression with a left-hand-side that is a matrix with one or two prototype indexes and a right hand side that can be any JSL expression using those indexes and the local variables from the list (and in JMP global: variables).
Example
The following example provides read access to the global namespace.
a = 42;
x = [1 2 3, 4 5 6, 7 8 9];
Show( Parallel Assign( {}, x[i, j] = global:a ) );
Show( x );
Parallel Assign({}, x[i,j] = global:a) = 1;
x =
[ 42 42 42,
42 42 42,
42 42 42];
Print Matrix(M, <named arguments>)
Description
Returns a quoted string that contains a well-formatted matrix. You can use the function, for example, to print the matrix to the log.
Argument
M
A matrix.
Optional Named Arguments
<<ignore locale(Boolean)
Set to false (0) to use the decimal separator for your locale. Set to true (1) to always use a period (.) as a separator. The default value is false (0).
<<decimal digits(n)
An integer that specifies the number of digits after the decimal separator to print.
<<style("style name")
Use one of three available styles: Parseable is a reformatted JSL matrix expression. Latex is formatted for LaTeX. If you specify Other, you must define the following three arguments.
<<separate("character")
Define the separator for concatenated entries.
<<line begin("character")
Define the beginning line character.
<<line end("character")
Define the ending line character.
QR(A)
Description
Returns the QR decomposition of A. Typical usage is {Q, R} = QR(A).
Random SVD(X, <nSingularValues=min(nRow, nCol)>, <nOver=10>, <nIter=2>)
Description
Computes the singular value decomposition (SVD) of matrix X using the randomized singular value decomposition. This decomposition can be faster than a traditional SVD, and it typically achieves an accurate approximation. It is particularly fast for large matrices when only a few singular values are desired. The method randomly projects the data into a low-dimensional space, performing the SVD in the low-dimensional space, and then computing an estimate of the SVD for the original data. The dimension of the computational space is equal to the number of singular values plus the number of oversampled columns.
Returns
Returns a list {U, M, V} such that U*diag(M)*V′ is equal to X.
Arguments
X
A matrix.
nSingularValues
The number of singular values to return. By default, this value is the minimum of the number of rows and number of columns in the matrix X.
nOver
The number of oversampled columns.
nIter
The number of power iterations.
Rank Index(vector)
Rank(vector)
Description
Returns a vector of indices that, used as a subscript to the original vector, sorts the vector by rank. Excludes missing values. Lists of numbers or quoted strings are supported in addition to matrices.
Ranking(vector)
Description
Returns a vector of ranks of the values of vector, low to high as 1 to n, ties arbitrary. Lists of numbers or quoted strings are supported in addition to matrices.
Ranking Tie(vector)
Description
Returns a vector of ranks of the values of vector, but ranks for ties are averaged. Lists of numbers or quoted strings are supported in addition to matrices.
Scoring Impute(rowWithMissing, VMat, colMeanVec, colStdDevVec)
Description
Provides streaming functionality for the Automated Data Imputation (ADI) algorithm.
Returns
Returns the row vector with the missing values imputed using the standard least squares estimation.
Arguments
rowwithMissing
A row vector that contains missing values.
VMat
A loading matrix that is produced by the ADI algorithm.
colMeanVec
A vector of the column means ignoring missing cells.
colStdDevVec
a vector of the column standard deviations ignoring missing cells.
Shape(A, nrow, <ncol>, < <<bycol>)
Description
Reshapes the matrix A across rows to the specified dimensions. Each value from the matrix A is placed into the reshaped matrix. By default, the values are placed row-by-row.
Returns
The reshaped matrix.
Arguments
A
A matrix.
nrow
The number of rows that the new matrix should have.
ncol
(Optional) The number of columns the new matrix should have.
<<bycol
(Optional) Specifies that the values be placed into the reshaped matrix column-by-column, instead of row-by-row.
Notes
If ncol is not specified, the number of columns is whatever is necessary to fit all of the original values of the matrix into the reshaped matrix.
If a missing value is specified for nrow, the number of rows is whatever is necessary to fit all of the original values of the matrix into the reshaped matrix.
If the new matrix is smaller than the original matrix, the extra values are discarded.
If the new matrix is larger than the original matrix, the values are repeated to fill the new matrix.
Examples
a = Matrix({ {1, 2, 3}, {4, 5, 6}, {7, 8, 9} });
[ 1 2 3,
4 5 6,
7 8 9]
Shape(a, 2);
[ 1 2 3 4 5,
6 7 8 9 1]
Shape(a, 2, 2);
[ 1 2,
3 4]
Shape(a, 4, 4);
[ 1 2 3 4,
5 6 7 8,
9 1 2 3,
4 5 6 7]
Shape(a, 4, 4, <<bycol);
[ 1 5 9 4,
2 6 1 5,
3 7 2 6,
4 8 3 7]
Solve(A, b)
Description
Solves a linear system. In other words, x=inverse(A)*b.
Sort Ascending(source)
Description
Returns a copy of a list or matrix source with the items in ascending order.
Sort Descending(source)
Description
Returns a copy of a list or matrix source with the items in descending order.
Sparse SVD(X, <nSingularValues=min(nRow, nCol)>, <tolerance=1e-10>)
Description
Computes the singular value decomposition (SVD) of matrix X using the implicitly restarted, partially reorthogonalized Lanczos method for sparse matrices.
Returns
Returns a list {U, M, V} such that U*diag(M)*V′ is equal to X.
Arguments
X
A matrix.
nSingularValues
The number of singular values to return. By default, this value is the minimum of the number of rows and number of columns in the matrix X.
tolerance
The tolerance for the convergence criterion.
Spline Coef(x, y, lambda)
Description
Returns a five column matrix of the form knots||a||b||c||d where knots is the unique values in x.
x is a vector of regressor variables, y is the vector of response variables, and lambda is the smoothing argument. Larger values for lambda result in smoother splines.
Spline Eval(x, coef)
Description
Evaluates the spline predictions using the coef matrix in the same form as returned by SplineCoef(), in other words, knots||a||b||c||d. The x argument can be a scalar or a matrix of values to predict. The number of columns of coef can be any number greater than 1 and each is used for the next higher power. The powers of x are centered at the knot values. For example, the calculation for coef of knots||a||b||c||d is j is such that knots[j] is the largest knot smaller than x.
xx = x-knots[j] is the centered x value:
result = a[j] + xx * (b[j] + xx * (c[j] + xx * d[j]))
The following line is equivalent:
result = a[j] + b[j] * xx + c[j] * xx ^ 2 + d[j] * xx ^ 3
Spline Smooth(x, y, lambda)
Description
Returns the smoothed predicted values from a spline fit.
x is a vector of regressor variables, y is the vector of response variables, and lambda is the smoothing argument. Larger values for lambda result in smoother splines.
SVD(A)
Description
Singular value decomposition.
Sweep(A, <indices>)
Description
Sweeps, or inverts a matrix a partition at a time.
Trace(A)
Description
The trace, or the sum of the diagonal elements of a square matrix.
Transpose(A)
Description
Transposes the rows and columns of the matrix A.
Returns
The transposed matrix.
Arguments
A
A matrix.
Equivalent Expression
A‘
V Concat(A, B, ...)
Description
Vertical concatenation of two or more matrices.
Returns
The new matrix.
Arguments
Two or more matrices.
V Concat To(A, B, ...)
Description
Vertical concatenation in place. This is an assignment operator.
Returns
The new matrix.
Arguments
Two or more matrices.
V Max(matrix)
Description
Returns a row vector containing the maximum of each column of matrix.
V Mean(matrix)
Description
Returns a row vector containing the mean of each column of matrix.
V Median(matrix)
Description
Returns a row vector containing the median of each column of matrix.
V Min(matrix)
Description
Returns a row vector containing the minimum of each column of matrix.
V Quantile(matrix, p)
Description
Returns a row vector containing the pth quantile of each column of matrix.
V Standardize(matrix)
Description
Returns a matrix column-standardized to mean = 0 and standard deviation = 1.
V Std(matrix)
Description
Returns a row vector containing the standard deviations of each column of matrix.
V Sum(matrix)
Description
Returns a row vector containing the sum of each column of matrix.
Varimax(matrix, <norm=1>)
Description
Performs a varimax rotation.
Returns
A list that contains the rotated matrix and the orthogonal rotation matrix.
Arguments
matrix
A matrix to be rotated.
norm
Specify 1 to perform a normalized rotation, and specify 0 to perform a non-normalized rotation. The default value is 1.
Vec Diag(A)
Description
Creates a vector from the diagonals of a square matrix A.
Returns
The new matrix.
Arguments
A
A square matrix.
Notes
Using a matrix that is not square results in an error.
Vec Quadratic(symmetric matrix, rectangular matrix)
Description
Constructs an n-by-m matrix. Used in calculation of hat values.
Returns
The new matrix.
Arguments
Two matrices. The first must be symmetric.
Equivalent Expression
Vec Diag(X*Sym*X‘)
VPTree(matrix)
Description
Returns a table using the vantage-point tree (VP tree) algorithm. The table can be used to efficiently look up nearest neighbors. The VP tree algorithm is particularly useful for wide data problems. The VP tree selects a random point as the vantage-point and partitions the remaining points based on their distance from it. The tree is built recursively and can be searched efficiently by checking distances and exploring relevant subtrees. By eliminating large portions of the search space, the vantage-point tree is useful for nearest neighbor search and other applications. For more information about the VP tree, see Uhlmann (1991).
Returns
A VPTree object.
Argument
matrix
A matrix of k-dimensional points. The number of dimensions or points is not limited. Each column in the matrix represents a dimension to the data, and each row represents a data point.
Messages
<<K nearest rows(stop, <position>)
Returns a matrix. <position> is a point that is described as a row vector for the coordinate of a row, or as the number of a row. If <position> is not specified, returns the n nearest rows and distances to all rows. If <position> is specified, returns the n nearest rows and distances to either a point or a row. Stop is either n or {n, limit}. The limit parameter defines the number of rows that will be returned. It can be specified one of two ways: a number, like 5, returns the 5 nearest rows. A list, like {5,10}, returns up to 5 nearest rows, stopping when the distance of 10 is exceeded. When using a list as limit, the last row returned may have a distance greater than 10. Because the command continues until it finds the closest row beyond the stop distance, this point is also returned. This can be especially useful if there are no rows within the stop distance.
Wavelet Basis Coef(x, grid, coeff, <wavelet = "Harr" | "Biorthogonal" | "Coiflet" | "Daubechies" | "Symlet">, <param = 0>)
Description
Finds the predictions for vector x for the specified Wavelet model.
Returns
A vector of predictions.
Arguments
x
A row or column vector that contains the data.
grid
A vector specifying the grid of the data.
coeff
A vector of wavelet coefficients.
wavelet
The name of the wavelet model.
param
An optional wavelet model parameter.
Notes
This function is used in column formulas created by the Functional Data Explorer platform.
Where(<dt>, clause)
Description
Filters and returns indices depending on the given clause. The clause can be a comparison function or a conditional statement. Columns, matrices, and lists can be mixed and matched within the same clause.
The indices returned by Where() are optimized for high performance on large lists, matrices, and columns.
Required Arguments
clause
A comparison function or conditional statement.
Optional Arguments
<dt>
Changes the current Data Table during the evaluation.
Examples
Names Default To Here( 1 );
xs = [10 20 30 . 50];
xs[Where( xs >= 20 )];
xs[Where( !Is Missing( xs ) )];
ys = {10, 20, "30", ., 50};
ys[Where( ys >= 20 )];