Principal Components
Reduce the Dimensionality of Your Data
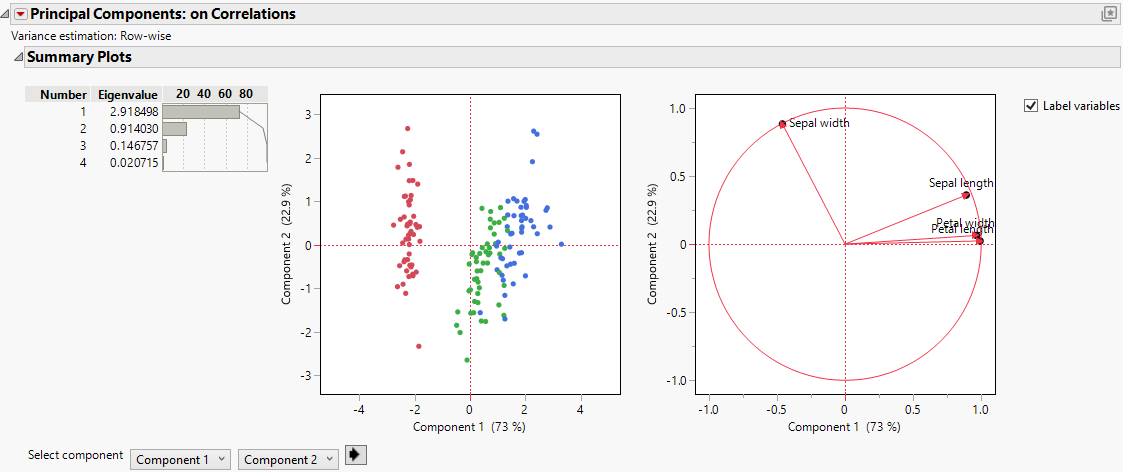
The purpose of principal component analysis is to derive a small number of independent linear combinations (principal components) of a set of measured variables that capture as much of the variability in the original variables as possible. Principal component analysis is a dimension-reduction technique, as well as an exploratory data analysis tool. Principal component analysis is also useful for constructing predictive models, as in principal components analysis regression (also known as PCA regression or PCR).
The Principal Components platform provides two categories of methods to obtain the principal components. The Traditional methods use the covariance matrix, correlation matrix, or unscaled and uncentered matrix to obtain the principal components. The Advanced methods use a variety of singular value decomposition techniques to obtain the principal components.
Advanced methods are useful for data with a vary large number of variables and enable you to calculate principal components with efficient computing times. Most of the advanced methods require you to specify the number of components to be estimated. This number is typically much smaller than the dimension of your data. These principal components can then be used in PCA regression.
The Principal Components platform also supports factor analysis. JMP offers several types of orthogonal and oblique factor analysis-style rotations to help interpret the extracted components. For factor analysis, see Factor Analysis.
Figure 4.1 Example of Principal Components