Statistical Details for Advanced Methods
This section contains statistical details for the estimation methods used when Advanced is specified as the Method Family in the Principal Components launch window. These methods are based on the singular value decomposition (SVD). This avoids calculating the covariance matrix, which makes them computationally efficient algorithms.
Full SVD
The Full SVD method uses an algorithm that is based on the full singular value decomposition of a matrix. Consider the following notation:
• n = number of rows
• p = number of variables
• X = n by p matrix of data values
The number of nonzero eigenvalues, and consequently the number of principal components, equals the rank of the correlation matrix of X. The number of nonzero eigenvalues cannot exceed the smaller of n and p.
The data are standardized prior to the implementation of the Full SVD method. To standardize a value, subtract its mean and divide by its standard deviation. Denote the n by p matrix of standardized data values by Xs. Then the covariance matrix of the standardized data is the correlation matrix of X and it is defined as follows:
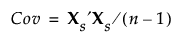
Using the singular value decomposition, Xs is written as UDiag(Λ)V′. This representation is used to obtain the eigenvectors and eigenvalues of Xs′Xs. The principal components, or scores, are given by XsV. For additional background information, see Wide Linear Methods and the Singular Value Decomposition.
Truncated SVD
The Truncated SVD method uses an algorithm that is based on the singular value decomposition, but does not implement a full decomposition. Instead, the algorithm computes only the first specified number of singular values and singular vectors in the singular value decomposition. Therefore, only the first specified number of eigenvalues and principal components are returned. For more information about the algorithm, see Baglama and Reichel (2005).
Randomized SVD
The Randomized SVD method uses an algorithm that is based on the singular value decomposition, but does not implement a full decomposition. The algorithm is a two-step process that involves low-rank matrix approximation. In general, the goal of low-rank matrix approximation is to approximate an m × p matrix A by finding m × k matrix B and k × p matrix C such that k is much smaller than p and A ≈ BC.
Consider the same notation that is described in Full SVD, where the goal is to decompose Xs.
In the first step of the Randomized SVD algorithm a matrix Q is found such that the following is true:
• Q has l orthonormal columns, where k ≤ l ≤ p
• Xs ≈ QQ′Xs
The details for efficiently computing a Q that has a few columns as possible can be found in Halko, Martinsson, and Tropp (2011).
The second step of the algorithm uses Q to compute the singular value decomposition of Xs. Let B = Q′Xs.Then, the following is true:
B = Q′Xs ⇒ QB = QQ′Xs ⇒ QB = Xs
Then, compute the SVD of B (which is much smaller than Xs):
B ≈ U*Diag(Λ)V′
QB ≈ (QU*)Diag(Λ)V′
A ≈ UDiag(Λ)V′, where U = QU*
For more information about the complete Randomized SVD algorithm, see Halko, Martinsson, and Tropp (2011).