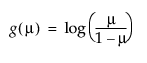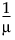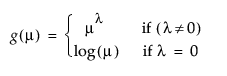Statistical Details for Generalized Linear Model Construction

Fitting Linear Models > Generalized Linear Models > Statistical Details for the Generalized Linear Model Personality > Statistical Details for Generalized Linear Model Construction

Publication date: 07/08/2024

Statistical Details for Generalized Linear Model Construction

To construct a generalized linear model, you must select response and explanatory variables for your data. You then must choose an appropriate link function and probability distribution for your response. Explanatory variables can be any combination of continuous variables, classification variables, and interactions. Some common examples of generalized linear models are listed in Table 13.1.

Table 13.1 Examples of Generalized Linear Models
Model	Response Variable	Distribution	Default Link Function
Traditional Linear Model	continuous	Normal	Identity(μ)
Logistic Regression	a count or a binary random variable	Binomial	Logit(μ)
Poisson Regression in Log Linear Model	a count	Poisson	Log(μ)
Exponential Regression	positive continuous	Exponential	Reciprocal(μ)

The platform fits a generalized linear model to the data by maximum likelihood estimation of the parameter vector. In general, there is no closed-form solution for the maximum likelihood estimates of the parameters. Therefore, the platform estimates the parameters of the model numerically through an iterative fitting process using a technique pioneered by Nelder and Wedderburn (1972). The overdispersion parameter φ is estimated by dividing the Pearson goodness-of-fit statistic by its degrees of freedom. Covariances, standard errors, and confidence limits are computed for the estimated parameters based on the asymptotic normality of maximum likelihood estimators.

A number of link functions and probability distributions are available in the Generalized Linear Model personality of the Fit Model platform. Table 13.2 lists the built-in link functions.

Table 13.2 Built-in Link Functions
Link Function Name	Link Function Formula
Identity	g(μ) = μ
Logit
Probit	g(μ) = Φ-1(μ), where Φ is the standard normal cumulative distribution function
Log	g(μ) = log(μ)
Reciprocal	g(μ) =
Power
Comp LogLog	g(m) = log(–log(1 – μ))

When you select the Power link function, a number box appears that enables you to enter the desired power.

Table 13.3 lists the variance functions associated with the available distributions for the response variable.

Table 13.3 Variance Functions for Response Distributions
Distribution	Variance Function
Normal	V(μ) = 1
Binomial	V(μ) = μ(1 – μ)
Poisson	V(μ) = μ
Exponential	V(μ) = μ2

Want more information? Have questions? Get answers in the JMP User Community (community.jmp.com).