Unequal Variances Reports
The Oneway platform provides four tests for equality of group variances. The concept behind the first three tests of unequal variances is to perform an analysis of variance on a new response variable constructed to measure the spread in each group. The fourth test is Bartlett’s test, which is similar to the likelihood ratio test under normal distributions. The Unequal Variances option is not available when a Block variable is specified in the launch window.
Note: Another method to test for unequal variances (also called heteroscedasticity) is ANOMV. See Analysis of Means Reports.
The following Tests for Equal Variances are available:
O’Brien
Constructs a dependent variable so that the group means of the new variable equal the group sample variances of the original response. An ANOVA on the O’Brien variable is actually an ANOVA on the group sample variances (O’Brien 1979; Olejnik and Algina 1987).
Brown-Forsythe
Shows the F test from an ANOVA where the response is the absolute value of the difference of each observation and the group median (Brown and Forsythe 1974).
Levene
Shows the F test from an ANOVA where the response is the absolute value of the difference of each observation and the group mean (Levene 1960). The spread is measured as 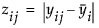 .
.
Bartlett
Compares the weighted arithmetic average of the sample variances to the weighted geometric average of the sample variances. The geometric average is always less than or equal to the arithmetic average with equality holding only when all sample variances are equal. The more variation there is among the group variances, the more these two averages differ. A function of these two averages is created, which approximates a χ2-distribution (or, in fact, an F distribution under a certain formulation). Large values correspond to large values of the arithmetic or geometric ratio, and therefore to widely varying group variances. Dividing the Bartlett Chi-square test statistic by the degrees of freedom gives the F value shown in the table. Bartlett’s test is not very robust to violations of the normality assumption (Bartlett and Kendall 1946).
F Test 2-sided
(Available only if there are two levels of the X variable.) If there are only two groups tested, then a standard F test for unequal variances is also performed. The F test is the ratio of the larger to the smaller variance estimate. The p-value from the F distribution is doubled to make it a two-sided test.
Note: If you have specified a Block column, then the variance tests are performed on data after it has been adjusted for the Block means.
See Example of the Unequal Variances Option.
Tip: If the unequal variances test reveals that the group variances are significantly different, consider Welch’s test instead of the standard ANOVA test. The Welch statistic is based on the usual ANOVA F test. However, the means are weighted by the reciprocal of the group mean variances (Welch 1951; Brown and Forsythe 1974; Asiribo and Gurland 1990). If there are only two levels, the Welch ANOVA is equivalent to an unequal variance t test.
Tests That the Variances Are Equal Report
In the Oneway platform, the Tests That the Variances Are Equal report shows a plot of standard deviations and provides summary tables. The first table contains the following columns:
Level
The factor levels occurring in the data.
Count
The frequencies of each level.
Std Dev
The standard deviations of the response for each factor level. The standard deviations are equal to the means of the O’Brien variable. If a level occurs only once in the data, no standard deviation is calculated.
MeanAbsDif to Mean
The mean absolute difference of the response and group mean. The mean absolute differences are equal to the group means of the Levene variable.
MeanAbsDif to Median
The absolute difference of the response and group median. The mean absolute differences are equal to the group means of the Brown-Forsythe variable.
The second table summarizes the tests for equal variances and contains the following columns:
Test
The name of each test.
F Ratio
The calculated F statistic. See Statistical Details for Tests That the Variances Are Equal.
DFNum
The degrees of freedom in the numerator. If a factor has k levels, the numerator has k - 1 degrees of freedom. Levels occurring only once in the data are not used in calculating test statistics for O’Brien, Brown-Forsythe, or Levene. The numerator degrees of freedom in this situation is the number of levels used in calculations minus one.
DFDen
The degrees of freedom used in the denominator. For O’Brien, Brown-Forsythe, and Levene, a degree of freedom is subtracted for each factor level used in calculating the test statistic. If a factor has k levels, the denominator degrees of freedom is n - k.
p-Value
The probability of obtaining an F-ratio value larger than the one calculated if the variances are equal across all levels.
Note: A warning appears if any level of the X variable contains fewer than 5 observations. For more information about the performance of the above tests with small sample sizes, see Brown and Forsythe (1974) and Miller (1972).
Welch’s Test Report
F Ratio
The F test statistic for the equal means test.
DFNum
The degrees of freedom in the numerator of the test. If a factor has k levels, the numerator has k - 1 degrees of freedom. Levels occurring only once in the data are not used in calculating the Welch ANOVA. The numerator degrees of freedom in this situation is the number of levels used in calculations minus one.
DFDen
The degrees of freedom in the denominator of the test. See Statistical Details for Tests That the Variances Are Equal.
Prob>F
The probability of obtaining an F value larger than the one calculated if the means are equal across all levels.
t Test
(Available only when the X variable has exactly two levels.) Shows the relationship between the F ratio and the t Test. Calculated as the square root of the F ratio.