Validation Set with Two or Three Values in Stepwise Regression
 If you specify a Validation column with two or three values, the Stepwise personality fits models based on the training set. Model fit statistics are reported for the validation and test sets. See Validation and Test Set Statistic Definitions for details about how these statistics are defined.
If you specify a Validation column with two or three values, the Stepwise personality fits models based on the training set. Model fit statistics are reported for the validation and test sets. See Validation and Test Set Statistic Definitions for details about how these statistics are defined.
If the response is continuous, the following statistics appear in the Stepwise Regression Control panel:
• RSquare Validation (also shown in the Step History report)
• RASE Validation
• RSquare Test (if there is a test set)
• RASE Test (if there is a test set)
If the response is binary nominal or ordinal, the following statistics appear in the Stepwise Regression Control panel:
• RSquare Validation (also shown in the Step History report)
• Avg Log Error Validation
• RSquare Test (if there is a test set)
• Avg Log Error Test (if there is a test set)
Max Validation RSquare
If you specify a validation column with two or three values in the Fit Model window, the Stopping Rule defaults to Max Validation RSquare. This rule attempts to find a model that maximizes the RSquare statistic for the validation set. The rule can be applied with the Direction set to Forward or Backward.
Note: Max Validation RSquare considers only the models defined by p-value entry (Forward direction) or removal (Backward direction). It does not consider all possible models.
You can use the Step button to enter terms one-by-one in the Forward direction or to remove them one-by one in the Backward direction. At any point, you can select a model by clicking the button to the right of RSquare Validation in the Step History report. The selection of model terms is updated in the Current Estimates report. This is the model that is used once you click Make Model or Run Model.
Forward Direction
In the Forward direction, Stepwise constructs successive models by adding terms based on the next smallest p-value.
If you click Go rather than Step, the process of entering terms proceeds automatically. Among the fitted models, the model that is considered best is listed last. This model is obtained by overlooking local dips in RSquare Validation. Specifically, it is the model with the largest RSquare Validation that can be followed by as many as ten models with lower RSquare Validation values. This model is designated by the terms Best in the Parameter column and Specific in the Action column. The button to the right of RSquare Validation selects this Best model, though you are free to change this selection.
Backward Direction
In the Backward direction, Stepwise constructs successive models by removing terms based on the next largest p-value.
To use the Backward direction, you must first click Enter All to enter all of the terms into the model. The Backward direction behaves in a similar fashion to the Forward direction. If you click Go rather than Step, the process of removing terms proceeds automatically. The model designated as Best is the one with the largest RSquare Validation that can be followed by as many as ten models with lower RSquare Validation values.
Validation and Test Set Statistic Definitions
RSquare Validation and RASE Validation are defined in this section. RSquare Test and RASE Test are computed for the test set in a completely analogous fashion.
Continuous Response
RSquare Validation
An RSquare measure for the validation set computed as follows:
– For each observation in the validation set, compute the prediction error. This is the difference between the actual response and the response predicted by the training set model.
– Square and sum the prediction errors to obtain SSEValidation.
– Square and sum the differences between the actual responses in the validation set and their mean. This is the SSTValidation.
– RSquare Validation is:
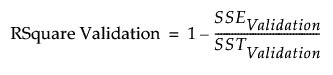
Note: It is possible for RSquare Validation to be negative.
RASE Validation
The square root of the mean squared prediction error for the validation set. This is computed as follows:
– For each observation in the validation set, compute the prediction error. This is the difference between the actual response and the response predicted by the training set model.
– Square and sum the prediction errors to obtain the SSEValidation.
– Denote the number of observations in the validation set by nValidation.
– RASE Validation is:
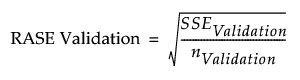
Binary Nominal or Ordinal Response
RSquare Validation
An Entropy RSquare measure (also known as McFadden’s R2) for the validation set computed as follows:
– A model is fit using the training set.
– Predicted probabilities are obtained for all observations.
– Using the predicted probabilities based on the training set model, the likelihood for the model is computed for observations in the validation set. Call this quantity Likelihood_FullValidation.
– Using the data in the validation set, the likelihood of the reduced model (no predictors) is computed. Call this quantity Likelihood_ReducedValidation.
– RSquare Validation is:
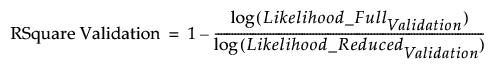
Note: It is possible for RSquare Validation to be negative.
Avg Log Error Validation
The average log error for the validation set is computed as follows:
– For each observation in the validation set, compute the log of its predicted probability as determined by the model based on the training set.
– Sum these logs, divide by the number of observations in the validation set, and take the negative of the resulting value.
Tip: Smaller values of Avg Log Error Validation are desirable.