Utilizzo della regressione con un predittore
Se si ha una variabile Y continua e una singola variabile X continua, è possibile costruire un modello di regressione semplice.
Scenario
Questo esempio utilizza la tabella di dati Companies.jmp, che contiene dati finanziari relativi a 32 società farmaceutiche e di informatica.
Intuitivamente, ha senso che le società con un maggior numero di dipendenti possano generare più ricavi rispetto alle società con un minor numero di dipendenti. Un analista desidera prevedere i ricavi complessivi derivanti dalle vendite per ciascuna società in base al numero dei dipendenti.
A tale scopo, eseguire le operazioni indicate in:
• Individuazione della relazione
• Stima del modello di regressione
• Previsione delle vendite medie
Individuazione della relazione
Innanzi tutto, creare un grafico a dispersione per osservare la relazione fra il numero dei dipendenti e la quantità di ricavi derivanti dalle vendite. Questo grafico a dispersione è stato creato in Creazione del grafico a dispersione. Dopo avere nascosto ed escluso un outlier (una società con un numero significativamente elevato di dipendenti e vendite rispetto alle altre), il grafico in Figura 5.12 mostra il risultato.
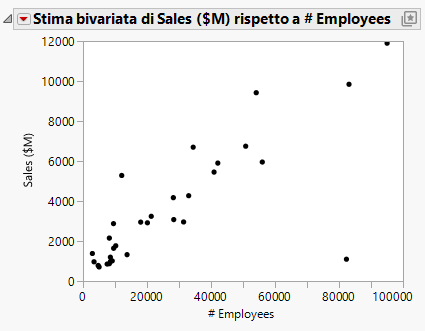
Figura 5.12 Grafico a dispersione di Sales ($M) rispetto a # Employees
Questo grafico a dispersione mostra chiaramente la relazione fra le vendite e il numero dei dipendenti. Come previsto, quanti più dipendenti ha una società, tante più vendite è in grado di generare. Ciò conferma visivamente l'ipotesi dell'analisi ma non prevede le vendite per un dato numero di dipendenti.
Stima del modello di regressione
Per prevedere i ricavi derivanti dalle vendite dal numero dei dipendenti, stimare un modello di regressione. Fare clic sul triangolo rosso associato a Stima bivariata e selezionare Stima lineare. Una linea di regressione viene aggiunta al grafico a dispersione e vengono aggiunti report alla finestra dei report.
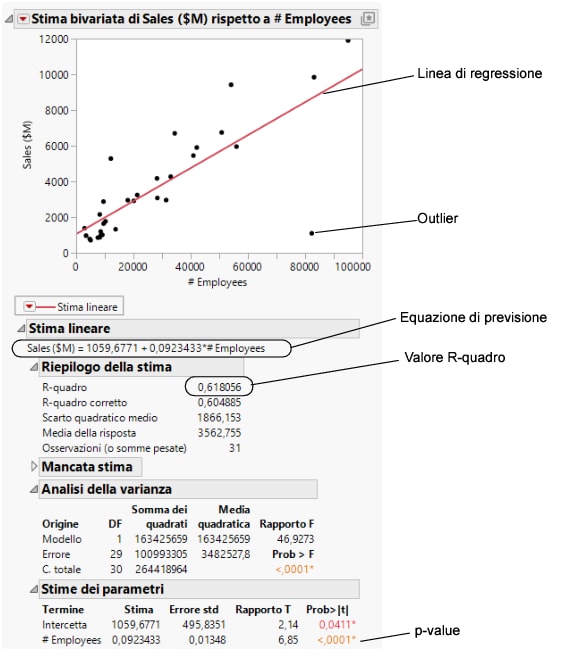
Figura 5.13 Linea di regressione
All'interno dei report, osservare i seguenti risultati:
• il p-value di <.0001
• il valore R-quadro 0.618
Da questi risultati, l'analista può concludere che:
• Il p-value del termine del modello #Employees è piccolo. Ciò significa che al livello di significatività di 0,05 il coefficiente di #Employees non è zero. Quindi, l'inserimento del numero dei dipendenti nel modello di previsione migliora sensibilmente la capacità di prevedere le vendite medie rispetto a un modello senza il numero dei dipendenti.
• Il valore R-quadro di 0,618 indica che questo modello spiega circa il 62% della variabilità nelle vendite. Il valore R-quadro è il coefficiente di determinazione e indica la proporzione della varianza nella variabile (di risposta) dipendente spiegata dal modello. R-quadro può avere un intervallo da 0 a 1. Un modello con un R-quadro pari a 0 non ha potenza esplicativa. Un modello con un R-quadro pari a 1 prevede la risposta perfettamente.
Previsione delle vendite medie
Utilizzare il modello di regressione per prevedere le vendite medie che una società potrebbe aspettarsi se avesse un certo numero di dipendenti. L'equazione di previsione per il modello è inclusa nel report:
Vendite medie = 1059,68 + 0,092*dipendenti
Per esempio, in una società con 70.000 dipendenti, si prevede che le vendite ammontino a $7.500:
$7.499,68 = 1059,68 + 0,092*70.000
Nell'area inferiore destra del grafico a dispersione corrente, è presente un outlier che non segue il pattern generale delle altre società. L'analista desidera sapere se il modello di previsione cambia quando questo outlier viene escluso.
Esclusione dell'outlier
1. Fare clic sull'outlier.
2. Selezionare Righe > Escludi/Annulla esclusione.
3. Per stimare questo modello, fare clic sul triangolo rosso associato a Stima bivariata di Sales (SM) By # Employees e selezionare Stima lineare.
I seguenti elementi vengono aggiunti alla finestra del report (Figura 5.14):
• una nuova linea di regressione
• un nuovo report Stima lineare, che comprende:
– una nuova equazione di previsione
– un nuovo valore R-quadro
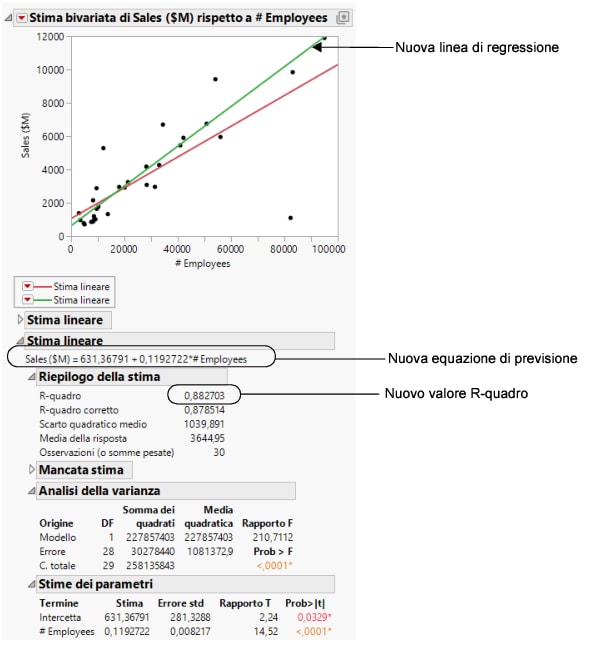
Figura 5.14 Confronto dei modelli
Interpretazione dei risultati
Utilizzando i risultati presenti in Figura 5.14, l'analista può trarre le seguenti conclusioni:
• L'outlier fa spostare la linea di regressione verso il basso per le società più grandi e verso l'alto per le società più piccole.
• Il nuovo modello per i dati senza l'outlier è un modello più forte rispetto al primo modello. Il nuovo valore R-quadro di 0,88 è maggiore e più vicino a 1 rispetto all'analisi iniziale.
Conclusioni
Utilizzando la nuova equazione di previsione, le vendite medie previste per una società con 70.000 dipendenti possono essere calcolate nel seguente modo:
$8961.37 = 631.37 + 0,119*70.000
La previsione del primo modello era di $7500. Il secondo modello prevede un totale di vendite di circa $8960 o un aumento di $1460 rispetto al primo modello.
Il secondo modello, dopo avere rimosso l'outlier, descrive e prevede totali delle vendite in base al numero dei dipendenti in un modo migliore rispetto al primo modello. L'analista ora dispone di un ottimo modello da utilizzare.