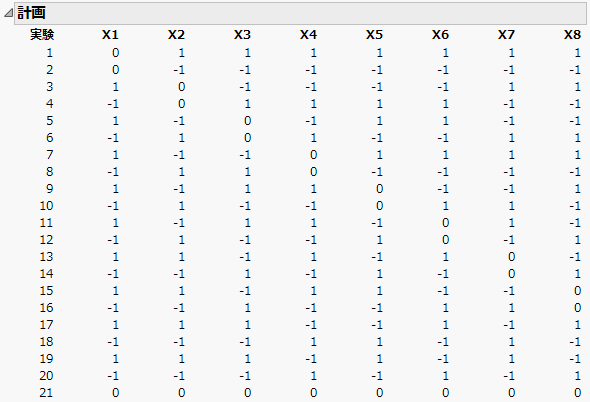
8つの連続変数の決定的スクリーニング計画は、連続尺度の8つの因子に対する決定的スクリーニング計画です。なお、偽因子（fake factor）を用いて、4回の実験を追加しています。次の点を確認してください。
図7.22 8つの連続変数の決定的スクリーニング計画
JMPの決定的スクリーニング計画は、カンファレンス行列（Xiao et al., 2012）を使用して作成されます。カンファレンス行列は、m x mの行列Cです（mは偶数）。行列Cは、対角要素が0、非対角要素が1または-1で、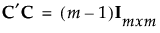
を満たしている行列です。
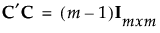を満たしている行列です。k個の因子がすべて連続尺度である場合について考えます。以下の説明では、カンファレンス行列が存在するものとして話を進めます。
|
•
|
kが偶数の場合、k x kのカンファレンス行列に基づいて計画を作成します。 元のカンファレンス行列に、その符号を逆にした行列–Cを追加します。さらに、計画に中心点を追加することにより、切片、主効果、2乗の効果を含んだモデルが推定可能となります。kが偶数の場合、このように計画を作成すると、決定的スクリーニング計画の最小の実験回数は2k + 1となります。
|
|
•
|
kが奇数の場合、(k+1) x (k+1)のカンファレンス行列を使用し、最後の列を削除します。そして、中心点を追加します。kが奇数の場合、このように計画を作成すると、スクリーニング計画の最小の実験回数は2k + 3となります。
|
因子の一部が2水準のカテゴリカルな因子である場合も、同様の方法で計画を作成します。以下の説明でも、カンファレンス行列が存在するものとして話を進めます。2水準のカテゴリカルな因子を含む決定的スクリーニング計画については、 Jones and Nachtsheim（2013）を参照してください。
|
•
|
|
•
|
kが奇数の場合、全体の実験回数は2k + 4となります。
|
カンファレンス行列が存在しないmの場合は、次に大きい偶数のカンファレンス行列に基づいて決定的スクリーニング計画が作成されます。その結果、全体の実験回数は、連続尺度の場合で2k + 3を超えることも、カテゴリカルの場合で2k + 4を超えることもあります。
実験で実際に調べる因子の個数を、kとしましょう。実験を追加するには、まず、k + k1個の因子について、第 “カンファレンス行列と実験回数”で説明した方法で計画を作成します。そして、最後のk1 列を削除します。たとえば、k1 = 2の場合は、4つの実験が追加されます。また、k1 = 4の場合は、8つの実験が追加されます。実験を4回追加するだけでも、モデル選択において非常に効果的です。