YFunction関数は、滑らかな連続関数を描くために使います。最初の引数は、プロットする式です。第2引数は、式の中のX変数の名前です。
win = New Window( "正弦関数",
Graph Box(
Frame Size( 200, 100 ),
X Scale( -10, 10 ),
Y Scale( -1, 1 ),
X Name( "x" ),
Y Name( "Sine(x)" ),
Y Function( Sine( x ), x ) ) );
図12.32 正弦波
Forループを使って、複数の正弦波を重ね合わせることもできます。
win = New Window( "重ね合わせた正弦波",
Graph Box(
Frame Size( 200, 100 ),
X Scale( -10, 10 ),
Y Scale( -1, 1 ),
For( i = 1, i <= 4, i += .1,
Y Function( Sine( x / i ), x )
)
)
);
図12.33 重ね合わせた正弦波
同様に、XFunctionを使うと、y変数の値の変化に従ってxの値が変化するグラフを描くことができます。
win = New Window( "重ね合わせた正弦波",
Graph Box(
Frame Size( 100, 200 ),
X Scale( -1, 1 ),
Y Scale( -10, 10 ),
For( i = 1, i <= 4, i += .2,
X Function( Sine( y / i ), y )
)
)
);
図12.34 X軸に沿って重ね合わせた正弦波
XY Function()は、第3の変数に依存する2つの計算式（パラメトリック方程式）を使って滑らかな曲線を描きます。第3変数の値は、最小値から最大値へと変化して、X-Yのペアを生成します。
win = New Window( "渦巻き",
Graph Box(
Pen Color( "red" ); // 線は赤色
xCenter = 50; // X軸における曲線の中心の位置
yCenter = 50; // Y軸における曲線の中心の位置
minAngle = 0;
maxAngle = Pi() * 2 * 20;
XY Function(
xCenter + ((ta / 3) * Cos( ta )),
yCenter + ((ta / 3) * Sin( ta )),
ta,
Min( minAngle ),
Max( maxAngle ),
Inc( Pi() / 100 )
);
)
);
図12.35 渦巻きのパラメトリックプロット
ContourFunction()は、2次元空間で3次元の関数を表現するための方法です。最後の引数には、等高線の値を指定します。単一の値や、::を使って作成した等間隔の値の行列、または任意の値の行列を指定できます。
win = New Window( "卵ケースの鳥瞰図",
Graph Box(
Frame Size( 300, 300 ),
X Scale( -10, 10 ),
Y Scale( -10, 10 ),
Pen Color( "black" );
Pen Size( 2 );
Contour Function( Sine( y ) + Cosine( x ), x, y, (0 :: 20) / 5 );
Pen Color( "red" );
Pen Size( 1 );
Contour Function( Sine( y ) + Cosine( x ), x, y, (-20 :: 0) / 5 );
)
);
図12.36 卵ケース
Normal Contour()は、2変量正規分布の等高線を描きます。k個の母集団を指定することができます。最初の引数は、等高線の確率を指定するスカラーまたは行列です。後続の引数は、平均、標準偏差、相関係数を指定する行列です。平均と標準偏差の行列の大きさはk × 2です。相関係数行列の大きさはk × 1で、最初の行は最初の等高線に対応し、2番目の行は2番目の等高線に対応し、以下同様に対応します。最初の列はx、2番目の列はyに対応します。次の例を見てみましょう。
Normal Contour(
[ prob1,
prob2,
prob3, ...],
[ xmean1 ymean1,
xmean2 ymean2,
xmean3 ymean3, ...],
[ xsd1 ysd1,
xsd2 ysd2,
xsd3 ysd3, ...],
[ xycorr1,
xycorr2,
xycorr3, ...]);
以下のスクリプトは、2母集団の2変量正規分布の累積確率0.1、0.5、0.7、および0.99における等高線を描きます。最初の母集団は、xの平均0、yの平均1、xの標準偏差0.3、yの標準偏差0.6、相関係数0.5です。2つ目の母集団は、xの平均4、yの平均6、xの標準偏差0.8、yの標準偏差0.4、相関係数0.9です。
win = New Window( "正規確率の等高線",
Graph Box(
X Scale( -5, 10 ),
Y Scale( -5, 10 ),
Normal Contour( [.1, .5, .7, .99], [0 1, 4 6], [.3 .6, .8 .4], [.5, .9] )
)
);
図12.37 Normal Contour関数
Normal Contour()は、二変量プラットフォームで作成できる確率楕円を作成する一般的な方法です。確率楕円を見るには、サンプルデータの「Football.jmp」を開き、「二変量の関係」のスクリプトを実行してください。
Gradient Function()は、式で指定された色でグリッド上の長方形を塗りつぶします。
Gradient Function( expression, xname, yname, [zlow, zhigh], ZColor( [colorLow, colorHigh] ), <XGrid( min, max, incr )>, <YGrid( min, max, incr )>, <Transparency( t )>;
Gradient Function()構文の要素の説明を以下に示します。
GradientFunction(
expression
// 等高線の式。式は、2変数の関数でなければならない
xname,yname,
// 式に含まれている2つの変数の名前
[zlow, zhigh],
// 式の上下限値。この2つの値を補間して色が決められる
ZColor([colorLow, colorHigh])
// 上限値と下限値それぞれに対応する色
<XGrid(min, max, incr),>
<YGrid(min, max, incr)> );
// グリッドの指定（オプション）
< Transparency >
// 値0はクリア（透明）を意味する 値1の場合は、完全に不透明になります（通常の描画モード）。
ZColor()値は名前ではなく数値コードでなければなりません。第 “色を指定する”に記載されているカラー表の番号を使うことができます（0=black（黒）、1=grey（グレー）、2=white（白）、3=red（赤）、4=green（緑）、5=blue（青）など）。
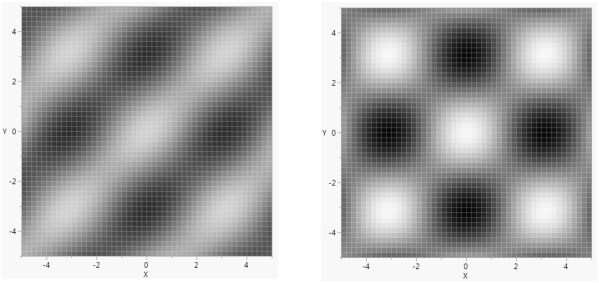
次の例では、Gradient Function()を使ってグラフのアニメーションを作成します。
phase = 0.7;
win = New Window( "Gradient Function",
a = Graph(
Frame Size( 400, 400 ),
X Scale( -5, 5 ),
Y Scale( -5, 5 ),
Gradient Function(
phase * Sine( x ) * Sine( y ) + (1 - phase) * Cosine( x ) * Cosine( y ),
x,
y,
[-1 1],
zcolor( [0, 2] )
)
)
);
b = a[FrameBox( 1 )];
For( i = 1, i <= 5, i++,
For( phase = 0, phase < 1, phase += 0.05,
b << Reshow;
Wait( 0.01 );
);
For( phase = 1, phase > 0, phase -= 0.05,
b << Reshow;
Wait( 0.01 );
);
);
図12.38 Gradient Function
